
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣ ![]() =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2 ![]() ,求满足条件的实数a的取值.
,求满足条件的实数a的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标 |
|
|
|
|
|
|
钻探深度 | 2 | 4 | 5 | 6 | 8 | 10 |
出油量 | 40 | 70 | 110 | 90 | 160 | 205 |
(1)在散点图中![]() 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即: ![]() )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: 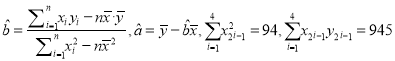 )
)
(3)设出油量与钻探深度的比值![]() 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号![]() 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 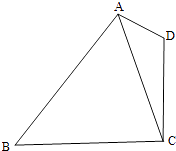
(Ⅰ)求cos∠CAD的值;
(Ⅱ)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个单位有职工800人,期中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
A.12,24,15,9
B.9,12,12,7
C.8,15,12,5
D.8,16,10,6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com