
【题目】已知函数![]() ,若
,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,且
,且![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】(i)当![]() 时,
时, ![]() ,令
,令![]() ,解得
,解得![]() ,函数
,函数![]() 有两个零点,舍去. (ii)当
有两个零点,舍去. (ii)当![]() 时,
时, ![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() .①当
.①当![]() 时,
时, ![]() ,当
,当![]() 或x>0时,f′(x)<0,此时函数f(x)单调递减;当
或x>0时,f′(x)<0,此时函数f(x)单调递减;当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 单调递增.∴
单调递增.∴![]() 是函数
是函数![]() 的极小值点,
的极小值点, ![]() 是函数
是函数![]() 的极大值点.∵函数
的极大值点.∵函数![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则:
,则: 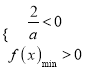 ,即:
,即: ![]() ,可得
,可得![]() .
.


②当![]() 时,
时, ![]() ,当
,当![]() 或
或![]() 时,
时, ![]() ,此时函数
,此时函数![]() 单调递增;当
单调递增;当![]() 时,f′(x)<0,此时函数
时,f′(x)<0,此时函数![]() 单调递减.∴
单调递减.∴![]() 是函数
是函数![]() 的极小值点,
的极小值点, ![]() 是函数
是函数![]() 的极大值点.不满足函数
的极大值点.不满足函数![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,综上可得:实数
,综上可得:实数![]() 的取值范围是
的取值范围是![]() .故选:C.
.故选:C.
点睛: 本题考查了利用导数研究函数的单调性极值与最值、函数的零点,考查了分类讨论方法、推理能力与计算能力.本题的解答方法是: (i)当![]() 时,
时, ![]() ,令
,令![]() ,解得
,解得![]() ,两个解,舍去. (ii)当
,两个解,舍去. (ii)当![]() 时,
时, ![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() .对
.对![]() 分类讨论:①当
分类讨论:①当![]() 时,由题意可得
时,由题意可得 ;②当
;②当![]() 时,推出极值点不满足题意,推出结果即可.
时,推出极值点不满足题意,推出结果即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤![]() (x+2)2成立.
(x+2)2成立.
(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-![]() x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y=![]() 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资![]() 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每![]() 长造价
长造价![]() 元,两侧墙砌砖,每
元,两侧墙砌砖,每![]() 长造价
长造价![]() 元,
元,
(1)求该仓库面积![]() 的最大值;
的最大值;
(2)若为了使仓库防雨,需要为仓库做屋顶.顶部每![]() 造价
造价![]() 元,求仓库面积
元,求仓库面积![]() 的最大值,并求出此时正面铁栅应设计为多长?
的最大值,并求出此时正面铁栅应设计为多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车收费标准如下:起步价![]() 元,起步历程为
元,起步历程为![]() (不超过
(不超过![]() 按起步价付费);超过
按起步价付费);超过![]() 但不超过
但不超过![]() ,超过部分按每千米
,超过部分按每千米![]() 元收费;超过
元收费;超过![]() 时,超过部分按每千米
时,超过部分按每千米![]() 元收费;另外每次乘坐需付燃油附加费
元收费;另外每次乘坐需付燃油附加费![]() 元.
元.
(1)写出乘车费用![]() (元)关于路程
(元)关于路程![]() (千米)的函数关系式;
(千米)的函数关系式;
(2)若某人一次出租车费用为31.15元,求此次出租车行驶了多少千米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学研究性学习是高中学生数学学习的一个有机组成部分,是在基础性、拓展性课程学习的基础上,进一步鼓励学生运用所学知识解决数学的和现实的问题的一种有意义的主动学习,是以学生动手动脑主动探索实践和相互交流为主要学习方式的学习研究活动.某同学就在一次数学研究性学习中发现,以下五个式子的值都等于同一个常数.
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() .
.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,归纳出一个三角恒等式;
(3)利用所学知识证明这个结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com