
 (其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8.
(其中x∈R,A>0,ω>0)的最大值为2,最小正周期为8. ,运算求得结果.
,运算求得结果. 运算求得结果.
运算求得结果. ,得
,得 .…(2分)
.…(2分) x+
x+ ).…(3分)
).…(3分) ,…(4分)
,…(4分) ,…(5分)
,…(5分) .
.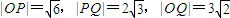 .…(8分)
.…(8分) .…(10分)
.…(10分) =
= .…(11分)
.…(11分) =
= .…(12分)
.…(12分) ,…(4分)
,…(4分) ,…(5分)
,…(5分)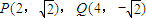 .
. ,即
,即 .…(7分)
.…(7分) .…(9分)
.…(9分) ,…(11分)
,…(11分) =
= .…(12分)
.…(12分)

科目:高中数学 来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版) 题型:解答题
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立;q:函数y=(m2-1)x是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省杭州市萧山中学高三(上)10月段考数学试卷(理科)(解析版) 题型:解答题
 (其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个点为
,且图象上一个点为 .
. 求函数f(x)的值域;
求函数f(x)的值域; 个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.
个单位,再将图象上各点的横坐标变为原来的2倍,纵坐标不变,求经以上变换后得到的函数解析式.查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市学军中学高三第二次月考数学试卷(文科)(解析版) 题型:选择题
 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省哈尔滨九中高考数学四模试卷(文科)(解析版) 题型:选择题
 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象查看答案和解析>>
科目:高中数学 来源:2010年天津市十二区县重点中学高三联考数学试卷1(理科)(解析版) 题型:选择题
 ,其中x∈R,则下列结论中正确的是( )
,其中x∈R,则下列结论中正确的是( )
 的图象左移
的图象左移 得到函数f(x)的图象
得到函数f(x)的图象查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com