
【题目】海南中学对高二学生进行心理障碍测试得到如下列联表:
焦虑 | 说谎 | 懒惰 | 总计 | |
女生 | 5 | 10 | 15 | 30 |
男生 | 20 | 10 | 50 | 80 |
总计 | 25 | 20 | 65 | 110 |
试说明在这三种心理障碍中哪一种与性别关系最大?
参考数据:K2= ![]()
P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10.828 |
【答案】解:由题设表格可得三个新的表格如下:
关于是否得到焦虑的结论:
焦虑 | 不焦虑 | 总计 | |
男生 | 5 | 25 | 30 |
女生 | 20 | 60 | 80 |
总计 | 25 | 85 | 110 |
关于是否说谎的结论:
说谎 | 不说谎 | 总计 | |
男生 | 10 | 20 | 30 |
女生 | 10 | 70 | 80 |
总计 | 20 | 90 | 110 |
关于是否懒惰的结论:
懒惰 | 不懒惰 | 总计 | |
男生 | 15 | 15 | 30 |
女生 | 50 | 30 | 80 |
总计 | 65 | 45 | 110 |
对于三种心理障碍分别构造三个随机变量k1 , k2 , k3 ,
由表中数据可得 ![]() ,
,![]() ,
,![]() ,
,
∴有97.5%的把握认为说谎与性别有关,没有充分数据显示焦虑和懒惰与性别有关,
这说明在这三种心理障碍中说谎与性别关系最大
【解析】由表中数据,将表分解为焦虑,说谎和懒惰三个表格,分别求得观测值k12 , k22 , k32 , 同题目所提供观测值表进行检验,比较大小,即可判断在这三种心理障碍中说谎与性别关系最大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+b满足f(1)=0,且在x=2时函数取得极值.
(1)求a,b的值;
(2)求函数f(x)的单调区间;
(3)求函数f(x)在区间[0,t](t>0)上的最大值g(t)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 是
是![]() 的中点,过
的中点,过![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于
于![]() 点.
点.

(1)证明:抛物线![]() 在
在![]() 点处的切线与
点处的切线与![]() 平行;
平行;
(2)是否存在实数![]() ,使以
,使以![]() 为直径的圆
为直径的圆![]() 经过
经过![]() 点?若存在,求出
点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的偶函数,当x>0时, ![]() .
.
(1)求f(x)的解析式;
(2)讨论函数f(x)的单调性,并求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=ax3﹣x2+cx(a≠0)的图象如图所示,它与x轴仅有两个公共点O(0,0)与A(xA , 0)(xA>0); 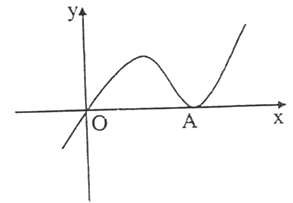
(1)用反证法证明常数c≠0;
(2)如果 ![]() ,求函数的解析式.
,求函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com