
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线与抛物线
且斜率为1的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的准线分别交于点
的准线分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式,方式一:周一到周五每天培训1小时,周日测试;方式二:周六一天培训4小时,周日测试.公司有多个班组,每个班组60人,现任选两组(记为甲组、乙组)先培训,甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如下表,其中第一、二周达标的员工评为优秀.
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
(1)在甲组内任选两人,求恰有一人优秀的概率;
(2)每个员工技能测试是否达标相互独立,以频率作为概率.
(i)设公司员工在方式一、二下的受训时间分别为![]() 、
、![]() ,求
,求![]() 、
、![]() 的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
的分布列,若选平均受训时间少的,则公司应选哪种培训方式?
(ii)按(i)中所选方式从公司任选两人,求恰有一人优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )
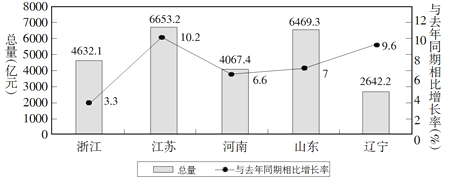
A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市民用水拟实行阶梯水价,每人用水量中不超过![]() 立方米的部分按4元/立方米收费,超出
立方米的部分按4元/立方米收费,超出![]() 立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
(1)如果![]() 为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,
为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米, ![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,估计该市居民该月的人均水费.
时,估计该市居民该月的人均水费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年11月21日,意大利奢侈品牌“![]() ﹠
﹠![]() ”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:
”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图;
,得到如图所示的频率分布直方图;

并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表.
一般关注 | 强烈关注 | 合计 | |
男 | 45 | ||
女 | 10 | 55 | |
合计 | 100 |
(1)在答题卡上补全列联表中数据;并判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)现已从“强烈关注”的网友中按性别分层抽样选取了5人,再从这5人中选取2人,求这2人中至少有1名女性的概率.
参考公式及数据:![]() ,
,
| 0.05 | 0.010 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正五边形![]() 的对角线
的对角线![]() 分别与对角线
分别与对角线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,对角线
,对角线![]() 分别与对角线
分别与对角线![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,对角线
,对角线![]() 与对角线
与对角线![]() 交于点
交于点![]() . 设由图2中的10个点
. 设由图2中的10个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和线段构成的等腰三角形的集合为
和线段构成的等腰三角形的集合为![]() .
.
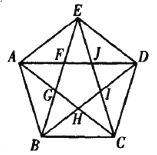
(1)求![]() 中元素的数目;
中元素的数目;
(2)若将这10个点中的每个点任意染为红、蓝两种颜色之一,问是否一定存在![]() 中的一个等腰三角形,其三个顶点同色?
中的一个等腰三角形,其三个顶点同色?
(3)若将这10个点中的任意![]() 个点染为红色,使得一定存在
个点染为红色,使得一定存在![]() 中的一个等腰三角形,其三个顶点同为红色,求
中的一个等腰三角形,其三个顶点同为红色,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com