
【题目】已知![]() ,
,![]() (
(![]() ,
,![]() ),
),![]() 且
且![]() 的图象上相邻两条对称轴之间的距离为
的图象上相邻两条对称轴之间的距离为![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() ,
,![]() 的值及
的值及![]() 边上的中线.
边上的中线.
【答案】(1)![]() .(2)
.(2)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由平面向量数量积的坐标运算,结合降幂公式及辅助角公式化简三角函数式,根据邻两条对称轴之间的距离求得![]() ,即可得函数
,即可得函数![]() 解析式,结合正弦函数的图象与性质即可求得
解析式,结合正弦函数的图象与性质即可求得![]() 的单调递增区间;
的单调递增区间;
(2)由![]() 代入解析式可得
代入解析式可得![]() 的值;由正弦定理与余弦定理,代入已知条件可得
的值;由正弦定理与余弦定理,代入已知条件可得![]() 的值;设AC边上的中线为BD,由
的值;设AC边上的中线为BD,由![]() ,结合平面向量数量积定义即可求得
,结合平面向量数量积定义即可求得![]() ,即为
,即为![]() 边上的中线长.
边上的中线长.
(1)由平面向量数量积的坐标运算,结合降幂公式及辅助角公式化简可得
![]()
![]()
![]()
![]()
由![]() 的图象上相邻两条对称轴之间的距离为
的图象上相邻两条对称轴之间的距离为![]() 得,
得,![]() ,
,
所以![]() .
.
令![]() 得,
得,
所以![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)![]()
解得![]() ,
,
由![]() 得
得![]() ,
,
由余弦定理可知![]() ,代入可得
,代入可得![]()
解得![]() ,
,![]()
记AC边上的中线为BD,

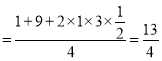 .
.
所以![]() ,即
,即![]() 边上的中线为
边上的中线为![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知菱形ABCD中,∠BAD=60°,AC与BD相交于点O.将△ABD沿BD折起,使顶点A至点M,在折起的过程中,下列结论正确的是( )
A.BD⊥CM
B.存在一个位置,使△CDM为等边三角形
C.DM与BC不可能垂直
D.直线DM与平面BCD所成的角的最大值为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B关于坐标原点O对称,![]() ,以M为圆心的圆过A,B两点,且与直线
,以M为圆心的圆过A,B两点,且与直线![]() 相切,若存在定点P,使得当A运动时,
相切,若存在定点P,使得当A运动时,![]() 为定值,则点P的坐标为( )
为定值,则点P的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节假期,旅游过年持续火爆.特别是:东北雪乡、梦回大唐、江南水乡、三亚之行这四条路线受到广大人民的热播.现有2个家庭准备去这四个地方旅游,假设每个家庭均从这四条路线中任意选取一条路线去旅源,则两个家庭选择同一路线的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点
过点![]() ,过抛物线E上一点
,过抛物线E上一点![]() 作两直线PM,PN与圆C:
作两直线PM,PN与圆C:![]() 相切,且分别交抛物线E于M、N两点.
相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据![]() 称为一个“好数据”,现从5个销售均价数据中任取
称为一个“好数据”,现从5个销售均价数据中任取
参考公式:回归方程系数公式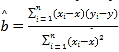 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央精准扶贫决策,某市将其低收入家庭的基本情况经过统计绘制如图,其中各项统计不重复.若该市老年低收入家庭共有900户,则下列说法错误的是( )

A.该市总有 15000 户低收入家庭
B.在该市从业人员中,低收入家庭共有1800户
C.在该市无业人员中,低收入家庭有4350户
D.在该市大于18岁在读学生中,低收入家庭有 800 户
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() 分别为
分别为![]() 的中点.
的中点.
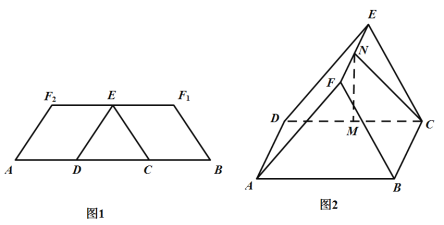
(1)证明:![]() 平面
平面![]()
(2)求几何体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com