
分析 (1)先求出sn,通过讨论n的范围,从而得到数列{an}的通项公式;
(2)通过讨论n的奇偶性,从而求出Tn的表达式,问题转化为使-$\frac{1}{9}$(2n2+6n)≥tn2(n为正偶数)恒成立即可;
(3)通过讨论公比的奇偶性,从而得到答案.
解答 解:(Ⅰ)由题意得f(x)=$\frac{1}{3}$(x+1)2-$\frac{1}{3}$,
∴Sn=$\frac{1}{3}$(n+1)2-$\frac{1}{3}$=$\frac{1}{3}$n2+$\frac{2}{3}$n(n∈N*),
当n≥2时,an=sn-sn-1=$\frac{1}{3}$n2+$\frac{2}{3}$n-[$\frac{1}{3}$(n-1)2+$\frac{2}{3}$(n-1)]=$\frac{2n+1}{3}$,
当n=1时,a1=s1=1适合上式,
∴数列{an}的通项公式是:an=$\frac{2n+1}{3}$(n∈N*);
(Ⅱ)∵bn=anan+1cos(n+1)π,(n∈N*),
∴Tn=b1+b2+…+bn
=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1anan+1,
由(Ⅰ)得:数列{an}是以1为首项,公差为$\frac{2}{3}$的等差数列,
①当n=2m,m∈N*时,
Tn=T2m=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1anan+1,
=a2(a1-a3)+a4(a3-a5)+…+a2m(a2m-1-a2m+1)
=-$\frac{4}{3}$(a2+a4+…+a2m)
=-$\frac{4}{3}$•$\frac{{a}_{2}+{a}_{2m}}{2}$•m
=-$\frac{1}{9}$(8m2+12m)
=-$\frac{1}{9}$(2n2+6n),
②当n=2m-1,m∈N*时,
Tn=T2m-1=T2m-(-1)2m-1a2ma2m+1
=-$\frac{1}{9}$(8m2+12m)+$\frac{1}{9}$(16m2+16m+3)
=$\frac{1}{9}$(8m2+4m+3)
=$\frac{1}{9}$(2n2+6n+7),
∴Tn=$\left\{\begin{array}{l}{-\frac{1}{9}(2{n}^{2}+6n),n为正偶数}\\{\frac{1}{9}(2{n}^{2}+6n+7),n为正奇数}\end{array}\right.$,要使Tn≥tn2对n∈N*恒成立,
只要使-$\frac{1}{9}$(2n2+6n)≥tn2(n为正偶数)恒成立,
即使-$\frac{1}{9}$(2+$\frac{6}{n}$)≥t对n为正偶数恒成立.
∴t≤[-$\frac{1}{9}$(2+$\frac{6}{n}$)]min=-$\frac{5}{9}$;
(Ⅲ)由an=$\frac{2n+1}{3}$知,数列{an}中每一项都不可能是偶数,
①如存在以a1为首项,公比q为2或4的数列{ank},k∈N*,此时{ank}中每一项除第一项外都是偶数,
故不存在以a1为首项,公比为偶数的数列{ank};
②q=1时,显然不存在这样的数列{ank},
q=3时,若存在以a1为首项,公比为3的数列{ank},k∈N*,则an1=1,
n1=1,ank=3k-1=$\frac{2{n}_{k}+1}{3}$,nk=$\frac{{3}^{k}-1}{2}$,
∴存在满足条件的数列{ank},且nk=$\frac{{3}^{k}-1}{2}$,(k∈N*).
点评 本题考查了二次函数的性质,考查了求数列的通项公式问题,考查函数恒成立问题,考查分类讨论思想,转化思想,通过讨论求出Tn的表达式,问题转化为函数恒成立是解答本题的关键,属于难题.


科目:高中数学 来源: 题型:选择题
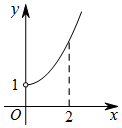 已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )| A. | $y=x+\frac{1}{x}$ | B. | y=log2|x| | ||
| C. | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x<0}\end{array}}\right.$ | D. | y=cos(2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $1+\sqrt{5}$ | B. | $2+\sqrt{5}$ | C. | $1+2\sqrt{5}$ | D. | $2+2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $6\sqrt{2}$ | C. | $4\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )| A. | 函数f(x)有极大值f(-2)和极小值f(2) | B. | 函数f(x)有极大值f(-3)和极小值f(1) | ||
| C. | 函数f(x)有极大值f(-3)和极小值f(3) | D. | 函数f(x)有极大值f(3)和极小值f(-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com