
【题目】从高三年级随机抽取100名学生,将他们的某次考试数学成绩绘制成频率分布直方图.由图中数据可知成绩在[130,140)内的学生人数为 . 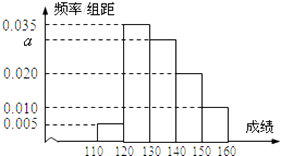
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】数列{an}的前项和为Sn , 且 ![]() ,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
,用[x]表示不超过x的最大整数,如[﹣0.1]=﹣1,[1.6]=1,设bn=[an],则数列{bn}的前2n项和b1+b2+b3+b4++b2n﹣1+b2n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
工种类别 | A | B | C |
赔付频率 | | | |
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.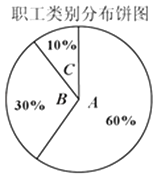
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,g(x)= ![]() +a.
+a.
(1)当a=2 时,求F(x)=f(x)﹣g(x)在(0,2]的最大值;
(2)讨论函数F(x)=f(x)﹣g(x) 的单调性;
(3)若f(x)g(x)≤0 在定义域内恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为( ) 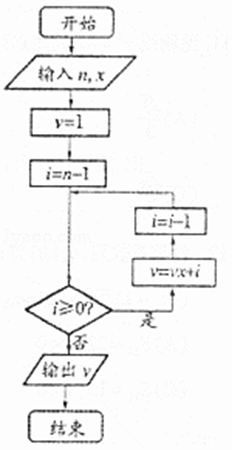
A.16
B.18
C.48
D.143
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若
=1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若 ![]() =λ
=λ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |+|
|+| ![]() |=8,则双曲线的标准方程为( )
|=8,则双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.![]() ﹣y2=1
﹣y2=1
C.![]() =1
=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体A﹣BCD中,AB=CD=10,AC=BD=2 ![]() ,AD=BC=2
,AD=BC=2 ![]() ,则四面体A﹣BCD外接球的表面积为( )
,则四面体A﹣BCD外接球的表面积为( )
A.50π
B.100π
C.200π
D.300π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com