
【题目】若关于x的方程x2﹣(a2+b2﹣6b)x+a2+b2+2a﹣4b+1=0的两个实数根x1 , x2满足x1≤0≤x2≤1,则a2+b2+4a的最小值和最大值分别为( )
A.![]() 和5+4
和5+4 ![]()
B.﹣ ![]() 和5+4
和5+4 ![]()
C.﹣ ![]() 和12
和12
D.﹣ ![]() 和15﹣4
和15﹣4 ![]()
【答案】B
【解析】解:令f(x)=x2﹣(a2+b2﹣6b)x+a2+b2+2a﹣4b+1,函数开口向上,又关于的方程x2﹣(a2+b2﹣6b)x+a2+b2+2a﹣4b+1=0的两个实数根x1 , x2满足x1≤0≤x2≤1,
得 ![]() ,即a2+b2+2a﹣4b+1≤0且a+b+1≥0
,即a2+b2+2a﹣4b+1≤0且a+b+1≥0
即(a+1)2+(b﹣2)2≤4且a+b+1≥0
表示以(﹣1,2)为圆心,半径小于等于2的圆平面与a+b+1=0右上部分平面区域的重叠部分
又a2+b2+4a=(a+2)2+b2﹣4
只要在满足条件区域中求点(a,b)到点(﹣2,0)距离最大最小即可
1)求最小
最小值为(﹣2,0)到a+b+1=0距离的平方减去4,得﹣ ![]()
2)求最大
最大值为(﹣2,0)与(﹣1,2)距离 ![]()
原式最大=( ![]() +2)2﹣4=5+4
+2)2﹣4=5+4 ![]()
故选B


科目:高中数学 来源: 题型:
【题目】已知从椭圆![]() 的一个焦点看两短轴端点所成视角为
的一个焦点看两短轴端点所成视角为![]() ,且椭圆经过
,且椭圆经过![]() .
.
(1)求椭圆的方程;
(2)是否存在实数![]() ,使直线
,使直线![]() 与椭圆有两个不同交点
与椭圆有两个不同交点![]() ,且
,且![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值.不存在,说明理由.
的值.不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.

(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一年级有学生![]() 名,高二年级有
名,高二年级有![]() 学生名.现用分层抽样方法(按高一年级、高二年级分二层)从该校的学生中抽取
学生名.现用分层抽样方法(按高一年级、高二年级分二层)从该校的学生中抽取![]() 名学生,调查他们的数学学习能力.
名学生,调查他们的数学学习能力.
(Ⅰ)高一年级学生中和高二年级学生中各抽取多少学生?
(Ⅱ)通过一系列的测试,得到这![]() 名学生的数学能力值.分别如表一和表二
名学生的数学能力值.分别如表一和表二
表一:
高一年级 |
|
|
|
|
|
人数 |
|
|
|
|
|
表二:
高二年级 |
|
|
|
|
|
人数 |
|
|
|
|
|
①确定![]() ,并在答题纸上完成频率分布直方图;
,并在答题纸上完成频率分布直方图;
②分别估计该校高一年级学生和高二年级学生的数学能力值的平均数(同一组中的数据用该组区间的中点值作代表);
③根据已完成的频率分布直方图,指出该校高一年级学生和高二年级学生的数学能力值分布特点的不同之处(不用计算,通过观察直方图直接回答结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在钝角△ABC中,∠A为钝角,令![]() ,若
,若![]() .现给出下面结论:
.现给出下面结论:
①当![]() 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;
;
③若点D在△ABC内部(不含边界),则![]() 的取值范围是
的取值范围是![]() ;
;
④若点D在线段BC上(不在端点),则![]()
⑤若![]() ,其中点E在直线BC上,则当
,其中点E在直线BC上,则当![]() 时,
时,![]() .
.
其中正确的有(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() f.
f.
(1)如果函数![]() 的单调递减区间为
的单调递减区间为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(3)若不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
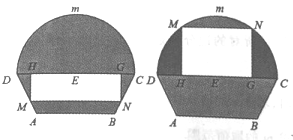
【题目】如图所示的自动通风设施.该设施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 为2米,梯形的高为1米,
为2米,梯形的高为1米, ![]() 为3米,上部
为3米,上部![]() 是个半圆,固定点
是个半圆,固定点![]() 为
为![]() 的中点.
的中点. ![]() 是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和
是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和![]() 平行.当
平行.当![]() 位于
位于![]() 下方和上方时,通风窗的形状均为矩形
下方和上方时,通风窗的形状均为矩形![]() (阴影部分均不通风).
(阴影部分均不通风).
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() (
(![]() 且
且![]() )米,试将通风窗的通风面积
)米,试将通风窗的通风面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数
的函数![]() ;
;
(2)当![]() 与
与![]() 之间的距离为多少米时,通风窗的通风面积
之间的距离为多少米时,通风窗的通风面积![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且满足4Sn﹣1=an2+2an , n∈N* .
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:
,数列{bn}的前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,BC边上的高AM所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0与BC相交于点P,若点B的坐标为(1,2).

(1)分别求AB和BC所在直线的方程;
(2)求P点坐标和AC所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com