
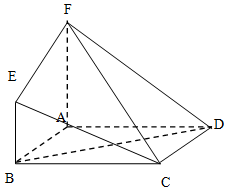
 已知空间几何体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.
已知空间几何体ABCDEF中,四边形ABCD是正方形,AF⊥平面ABCD,BE⊥平面ABCD,AB=AF=2BE.分析 (1)取AF的中点G连结BG,GD,EG,证明BG∥EF,CD∥EG,CE∥DG,结合CE∩EF=E,BG∩DG=G,得到平面BDG∥平面CEF,推出BD∥平面CEF.
(2)设AB=a,连结BF,说明∠BFC为CF与平面ABEF所成角的平面角,在Rt△CBF中,求解即可.
解答 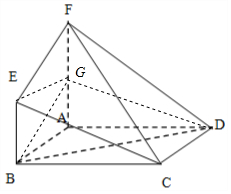 (1)证明:取AF的中点G连结BG,GD,EG
(1)证明:取AF的中点G连结BG,GD,EG
∵AF⊥平面ABCD,BE⊥平面ABCD,
∴BE∥GF且BE=GF,∴四边形BEFG为平行四边形,
∴BG∥EF,
同理可证四边形ABEG为平行四边形,∴EG∥AB且EG=AB,
又CD∥AB且CD=AB,∴CD∥EG且CD=EG,∴四边形CDGE为平行四边形,∴CE∥DG且EG=AB,
又∵CE∩EF=E,BG∩DG=G,∴平面BDG∥平面CEF,
∴BD∥平面CEF…(6分)
(2)解:设AB=a,则$AC=\sqrt{2}a,\;CF=\sqrt{3}a$,
连结BF,易证CB⊥平面ABEF,∴∠BFC为CF与平面ABEF所成角的平面角,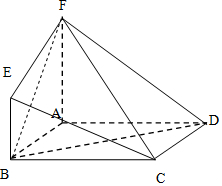
在Rt△CBF中,$sin∠BFC=\frac{BC}{CF}=\frac{AB}{CF}=\frac{a}{{\sqrt{3}a}}=\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查直线与平面所成角,直线与平面平行,平面与平面平行的判定定理与性质定理的应用,考查空间想象能力以及计算能力.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有 缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y+2)2=1 | B. | (x-1)2+(y-2)2=1 | C. | (x-1)2+(y+2)2=1 | D. | (x+1)2+(y-2)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com