
【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:1)设“中三等奖”为事件A,“中奖”为事件B,利用列举法能求出中三等奖的概率.(2)利用列举法求出中奖的概率,由此能求出不中奖的概率.
试题解析:
设“中三等奖”为事件A,“中奖”为事件B,
从四个小球中有放回地取两个有(0,0),(0,1),(0,2),(0,3), (1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3),共16种不同的结果.
(1)取出的两个小球号码相加之和等于4或3的取法有:(1,3),(2,2),(3,1),(0,3),(1,2),(2,1),(3,0),共7种结果,
则中三等奖的概率为P(A)=![]() .
.
(2)由(1)知两个小球号码相加之和等于3或4的取法有7种;
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2).
两个小球号码相加之和等于6的取法有1种:(3,3).
则中奖概率为P(B)=![]() =
=![]() .
.
所以不中奖的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为实数,函数
为实数,函数![]() .
.
(1)求证: ![]() 不是
不是![]() 上的奇函数;
上的奇函数;
(2)若![]() 是
是![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的值;
的值;
(3)若函数![]() 在区间
在区间![]() 上恰有3个不同的零点,求实数
上恰有3个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
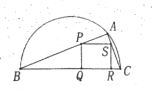
【题目】如图,某市园林局准备绿化一块直径为![]() 的半圆空地,
的半圆空地,![]() 以外的地方种草,
以外的地方种草,![]() 的内接正方形
的内接正方形![]() 为一水池,其余的地方种花,若
为一水池,其余的地方种花,若![]() 为定值),
为定值),![]() ,设
,设![]() 的面积为
的面积为![]() ,正方形
,正方形![]() 的面积为
的面积为![]()
(1)用![]() 表示
表示![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 取得最大值,并求出此最大值.
取得最大值,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() 、
、![]() 为常数).
为常数).
(Ⅰ)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当函数![]() 在
在![]() 处取得极值
处取得极值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com