
【题目】已知△ABC的两个顶点A,B的坐标分别为(﹣2,0),(2,0),且AC,BC所在直线的斜率之积等于![]() .
.
(1)求顶点C的轨迹方程;
(2)若斜率为1的直线![]() 与顶点C的轨迹交于M,N两点,且|MN|=
与顶点C的轨迹交于M,N两点,且|MN|=![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高级中学今年高一年级招收“国际班”学生![]() 人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这
人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这![]() 人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名,抽到第一批次、第二批次中女学生的概率分别是
名,抽到第一批次、第二批次中女学生的概率分别是![]() .
.
(1)求![]() 的值;
的值;
(2)为了检验研修的效果,现从三个批次中按分层抽样的方法抽取![]() 名同学问卷调查,则三个批次被选取的人数分别是多少?
名同学问卷调查,则三个批次被选取的人数分别是多少?
(3)若从第(2)小问选取的学生中随机选出两名学生进行访谈,求“参加访谈的两名同学至少有一个人来自第一批次”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和动点
和动点![]() ,以线段
,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)已知点![]() ,
, ![]() ,经过点
,经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.

(1)试计算出图案中圆柱与球的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换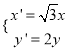 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 函数
函数![]() ,其图象的两条相邻对称轴间的距离为
,其图象的两条相邻对称轴间的距离为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,再将图象向右平移
,纵坐标不变,再将图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象,求
的图象,求![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com