
【题目】已知甲、乙两组数据的茎叶如图所示,若它们的平均数相同,则下列关于甲、乙两组数据稳定性的描述,正确的是( ) 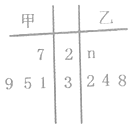
A.甲较稳定
B.乙较稳定
C.二者相同
D.无法判断
【答案】B
【解析】解:根据茎叶图得,甲的平均数是 ![]() =
= ![]() ×(27+31+35+39)=33, 乙的平均数是
×(27+31+35+39)=33, 乙的平均数是 ![]() =
= ![]() ×(20+n+32+34+38)=33,解得n=8,
×(20+n+32+34+38)=33,解得n=8,
∴甲的方差 ![]() =
= ![]() ×[(27﹣33)2+(31﹣33)2+(35﹣33)2+(39﹣33)2]=20,
×[(27﹣33)2+(31﹣33)2+(35﹣33)2+(39﹣33)2]=20,
乙的方差 ![]() =
= ![]() ×[(28﹣33)2+(32﹣33)2+(34﹣33)2+(38﹣33)2]=13,
×[(28﹣33)2+(32﹣33)2+(34﹣33)2+(38﹣33)2]=13,
∵ ![]() >
> ![]() ,
,
∴乙组数据较稳定.
故选:B.
【考点精析】根据题目的已知条件,利用茎叶图的相关知识可以得到问题的答案,需要掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少.


科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(3)求函数![]() 在定义域上的最大值及最小值,并求出函数取最值时
在定义域上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为:x2+y2﹣2x﹣4y+m=0.
(1)求m的取值范围;
(2)若圆C与直线3x+4y﹣6=0交于M、N两点,且|MN|=2 ![]() ,求m的值;
,求m的值;
(3)设直线x﹣y﹣1=0与圆C交于A、B两点,是否存在实数m,使得以AB为直径的圆过原点,若存在,求出实数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={(x,y)|y= ![]() },N={(x,y)|x﹣y+m=0},若M∩N的子集恰有4个,则m的取值范围是( )
},N={(x,y)|x﹣y+m=0},若M∩N的子集恰有4个,则m的取值范围是( )
A.(﹣2 ![]() ,2
,2 ![]() )
)
B.[﹣2,2 ![]() )
)
C.(﹣2 ![]() ,﹣2]
,﹣2]
D.[2,2 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 
附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)求x的值并估计全校3000名学生中读书谜大概有多少?(经频率视为频率)
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过抛物线C的焦点,且与C的对称轴垂直.l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )
A.18
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ex﹣alnx(其中a∈R,e为自然常数)
①a∈R,使得直线y=ex为函数f(x)的一条切线;
②对a<0,函数f(x)的导函数f′(x)无零点;
③对a<0,函数f(x)总存在零点;
则上述结论正确的是 . (写出所有正确的结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com