
| A. | (-1,0)∪(0,1) | B. | (-∞,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
分析 构造函数h(x)=f(x)•g(x),根据导数和函数单调性之间的关系,判断函数h(x)的单调性,结合函数的奇偶性的性质即可得到结论.
解答 解:设h(x)=f(x)•g(x),
∵x<0时,f′(x)g(x)+f(x)g′(x)>0,
即[f(x)g(x)]′>0
故h(x)在x<0时递增,
∵f(x)、g(x)分别是定义在R上的奇函数和偶函数,
∴h(x)=f(x)g(x)是R上的奇函数,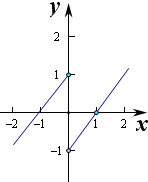
∴h(x)的图象关于原点对称,
即h(x)在x>0时也是增函数.
∵g(-1)=0,∴g(1)=0,
∴h(-1)=0且h(1)=0,则函数h(x)对应的草图为:
则h(x)>0的解集为:x>1或-1<x<0.
故不等式的解集为{x|x>1或-1<x<0},
故选:C.
点评 本题考查了函数的奇偶性的应用,以及导数的运算,不等式的解法等,根据导数的正负可以确定函数的单调性,利用数形结合的思想进行解题.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(1)>\frac{f(2)}{e^2}$ | B. | $f(1)<\frac{f(2)}{e^2}$ | C. | f(-2)>e3f(1) | D. | f(-2)<e3f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
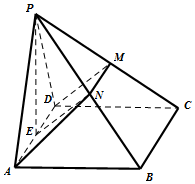 在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.
在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB的中点,过A、D、N三点的平面交PC于M,E为AD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com