
【题目】车间将10名技工平均分成甲乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为10.
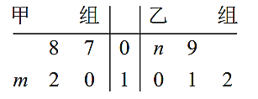
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)质检部门从该车间甲乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率;
(3)根据以上茎叶图和你所学的统计知识,分析两组技工的整体加工水平及稳定性.
(注:方差![]() ,其中
,其中![]() 为数据
为数据![]() ,
,![]() ,…,
,…,![]() 的平均数).
的平均数).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)甲乙两组的整体水平相当,乙组更稳定一些.
;(3)甲乙两组的整体水平相当,乙组更稳定一些.
【解析】
(1)由两组技工在单位时间内加工的合格零件平均数都为10.利用茎叶图能求出![]() ,
,![]() .
.
(2)质监部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,设两人加工的合格零件数分别为![]() ,利用列举法能求出该车间“质量合格”的概率.
,利用列举法能求出该车间“质量合格”的概率.
(3)先分别求出![]() ,
,![]() ,由两组技工在单位时间内加工的合格零件平均数都为10,
,由两组技工在单位时间内加工的合格零件平均数都为10,![]() ,得到乙组技工加工水平高.
,得到乙组技工加工水平高.
解:(1)根据题意可得:![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
(2)设事件![]() “该车间“质量合格””,
“该车间“质量合格””,
质监部门从该车间甲乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,设两人加工的合格零件数分别为![]() ,则所有的
,则所有的![]() 有
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共计25个,
,共计25个,
而![]() 的基本事件有
的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共计5个基本事件,故满足
,共计5个基本事件,故满足![]() 的基本事件共有
的基本事件共有![]() ,即该车间“质量合格”的基本事件有20个,
,即该车间“质量合格”的基本事件有20个,
∴![]() ,即该车间“质量合格”的概率为
,即该车间“质量合格”的概率为![]() .
.
(3)根据题意可得:
![]()
![]() ,
,
![]()
![]() ,
,
∵![]() ,
,![]() ,∴甲乙两组的整体水平相当,乙组更稳定一些.
,∴甲乙两组的整体水平相当,乙组更稳定一些.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() .
.
(1)求椭圆C的离心率;
(2)设![]() 分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线
分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线![]() 相交于点M,N.当点P运动时,以M,N为直径的圆是否经过
相交于点M,N.当点P运动时,以M,N为直径的圆是否经过![]() 轴上的定点?试证明你的结论.
轴上的定点?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“互联网+”是“智慧城市”的重要内容,A市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费WiFi为了解免费WiFi在A市的使用情况,调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有90%的把握认为A市使用免费WiFi的情况与年龄有关;
(2)将频率视为概率,现从该市45岁以上的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“偶尔或不用免费WiFi”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,数学期望E(X)和方差D(X).附:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 分别是棱
分别是棱![]() 的中点 .
的中点 .
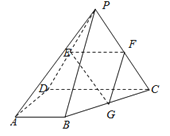
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 平面
平面![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
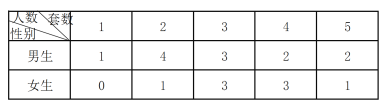
(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?
(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试判断男学生完成套卷数的方差![]() 与女学生完成套卷数的方差
与女学生完成套卷数的方差![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com