练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    过椭圆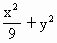＝1的左焦点作直线和椭圆交于A，B两点，若弦AB的长恰好等于短轴长，求这直线的方程．

    答案：
    解析：

    解：由椭圆方程知a＝3，b＝1，c＝2，(－2，0)，设直线方程为y＝k(x＋2)，代入椭圆方程得(1＋9)－9＝0，设A()，B()，则

    由|AB|＝＝·＝＝2，得直线AB的方程为x±y＋2＝0．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：学习周报　数学　人教课标高二版(A选修2－1)　2009－2010学年　第17期　总第173期 人教课标版(A选修2－1) 题型：022

    过椭圆＝1(a＞b＞0)的左焦点F1作x轴的垂线，交椭圆于点P，F2为右焦点，若∠F1PF2＝60°，则椭圆的离心率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    过椭圆+＝1的左焦点F1, 作垂直于长轴的直线交椭圆于A、B两点, F2为右焦点, 则│AF2│＝_________.(用假分数表示.)

    查看答案和解析>>

    科目：高中数学 来源：2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型：044

    设F1，F2分别是椭圆(a＞b＞0)的左，右焦点．

    (1)当a＝2b，点P在椭圆上，且PF1⊥PF2，|PF1|·|PF2|＝2时，求椭圆方程；

    (2)对于(1)中的椭圆，若直线x＝t(t≠0)分别交椭圆于P，Q两点，设椭圆的长轴顶点分别为A1，A2求直线A1P与A2Q交点的轨迹方程；

    (3)过(2)中轨迹的一个焦点作直线与轨迹交于A，B两点，若|AB|＝4，这样的直线能作几条？并证明你的结论？

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学理科(江西卷) 题型：013

    过椭圆＝1(a＞b＞0)的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2＝60°，则椭圆的离心率为

    [　　]

    A．

    B．

    C．

    D．

    查看答案和解析>>

    同步练习册答案