练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】“克拉茨猜想”又称“猜想”，是德国数学家洛萨克拉茨在年世界数学家大会上公布的一个猜想：任给一个正整数，如果是偶数，就将它减半；如果为奇数就将它乘加，不断重复这样的运算，经过有限步后，最终都能够得到，得到即终止运算，己知正整数经过次运算后得到，则的值为（ ）

    A.或B.或C.D.或或

    【答案】A

    【解析】

    设经过第次运算后变为，可知，，，，，经过逆向运算，逐步推导可依次得出、、、，并对分奇数和偶数两种情况分类讨论，进而可求得的值.

    设经过第次运算后变为，可知，，，，

    ，则，，

    若为奇数，则，得，不合乎题意，所以，为偶数，且.

    若为奇数，则，得，不合乎题意；

    若为偶数，则.

    若为奇数，则，可得；

    若为偶数，则.

    综上所述，或.

    故选：A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图1，四边形ABCD为等腰梯形，AB＝4，AD＝DC＝CB＝2，△ADC沿AC折起，使得平面ADC⊥平面ABC，E为AB的中点，连接DE，DB（如图2）.

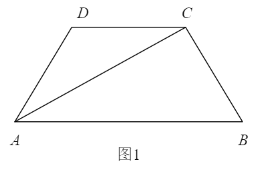
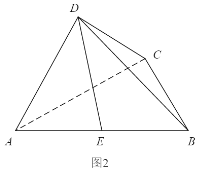
    （1）求证：BC⊥AD

    （2）求直线DE与平面BCD所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】口袋中有大小、形状、质地相同的两个白球和三个黑球．现有一抽奖游戏规则如下：抽奖者每次有放回的从口袋中随机取出一个球，最多取球2n＋1(n)次．若取出白球的累计次数达到n＋1时，则终止取球且获奖，其它情况均不获奖．记获奖概率为．

    （1）求；

    （2）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，抛物线上的点到准线的最小距离为.

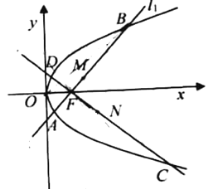
    （1）求抛物线的方程；

    （2）若过点作互相垂直的两条直线、，与抛物线交于两点，与抛物线交于两点，分别为弦的中点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春季，某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车，现有采购成本分别为11万元/辆和8万元/辆的A，B两款车型，根据以往这两种出租车车型的数据，得到两款出租车型使用寿命频数表如表：

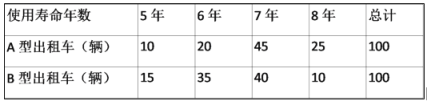
    （1）填写如表，并判断是否有99%的把握认为出租车的使用寿命年数与汽车车有关？

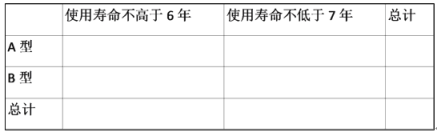
    （2）以频率估计概率，从2020年生产的A和B的车型中各随机抽1车，以X表示这2车中使用寿命不低于7年的车数，求X的分布列和数学期望；

    （3）根据公司要求，采购成本由出租公司负责，平均每辆出租每年上交公司6万元，其余维修和保险等费用自理，假设每辆出租车的使用寿命都是整数年，用频率估计每辆出租车使用寿命的概率，分别以这100辆出租车所产生的平均利润作为决策依据，如果你是该公司的负责人，会选择采购哪款车型？

    参考公式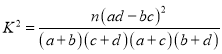：，其中n＝a+b+c+d.

    参考数据：

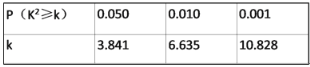
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司A产品生产的投入成本x（单位：万元）与产品销售收入y（单位：十万元）存在较好的线性关系，下表记录了该公司最近8次该产品的相关数据，且根据这8组数据计算得到y关于x的线性回归方程为．

    x（万元）

    6

    7

    8

    11

    12

    14

    17

    21

    y（十万元）

    1.2

    1.5

    1.7

    2

    2.2

    2.4

    2.6

    2.9

    （1）求的值（结果精确到0.0001），并估计公司A产品投入成本30万元后产品的销售收入（单位：十万元）．

    （2）该公司B产品生产的投入成本u（单位：万元）与产品销售收入v（单位：十万元）也存在较好的线性关系，且v关于u的线性回归方程为．

    （i）估计该公司B产品投入成本30万元后的毛利率（毛利率）；

    （ii）判断该公司A，B两个产品都投入成本30万元后，哪个产品的毛利率更大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】交强险是车主必须为机动车购买的险种，实行的是费率浮动机制，保费与上一年度车辆发生道路交通事故的情况相联系.每年交强险最终保险费计算方法是：交强险最终保险费，其中a为交强险基础保险费，A为与道路交通事故相联系的浮动比率，同时满足多个浮动因素的，按照向上浮动或者向下浮动比率的高者计算.按照我国《机动车交通事故责任强制保险基础费率表》的规定：普通6座以下私家车的交强险基础保险费为950元，交强险费率浮动因素及比率如下表：

    交强险浮动因素和浮动费率比率表

    类型

    浮动因素

    浮动比率

    上一个年度未发生有责任道路交通事故

    上两个年度未发生有责任道路交通事故

    上三个及以上年度未发生有责任道路交通事故

    上一个年度发生一次有责任不涉及死亡的道路交通事故

    上一个年度发生两次及以上有责任道路交通事故

    上一个年度发生有责任道路交通死亡事故

    某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况，统计结果如下表：

    类型

    数量

    25

    10

    10

    25

    20

    10

    以这100辆该品牌车的投保类型的频率代替一辆车投保类型的概率，完成下列问题.

    （1）记X为一辆该品牌车在第四年续保时的费用，求X的分布列与数学期望（数学期望值保留到个位数字）；

    （2）某二手车销售商专门销售这一品牌的二手车，且将经销商购车后下一年的交强险最终保险费高于交强险基础保险费的车辆记为事故车，假设购进一辆事故车亏损3000元，购进一辆非事故车盈利5000元.

    ①若该销售商购进三辆（车龄已满三年）该品牌二手车，求这三辆车中至少有一辆是事故车的概率；

    ②若该销售商一次购进100辆（车龄已满三年）该品牌二手车，求他获得利润的期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的极值点的个数；

    （2）若有3个极值点，，（其中），证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论在定义域内的极值点的个数；

    （2）若对，恒成立，求实数的取值范围；

    （3）证明：若，不等式成立.

    查看答案和解析>>

    同步练习册答案