解:(1)∵
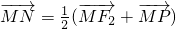
,∴点N是线段PF
2的中点
∵
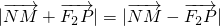
,
∴
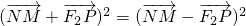
,化简可得
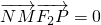
∴NM⊥PF
2,可得MN是线段PF
2的垂直平分线
∴
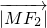
=
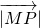
,可得
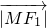
+
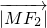
=

=4
因此,点M的轨迹是以F
1、F
2为焦点的椭圆,长轴2a=4,焦距2c=1,可得b
2=a
2-c
2=3
椭圆方程为

+

=1,即为点M的轨迹C的方程;
(2)设直线l的方程为y=kx+n,与椭圆

+

=1消去y,得(3+4k
2)x
2+8knx+4n
2-12=0
可得根的判别式△=64k
2n
2-16(3+4k
2)(4n
2-12)>0,化简得4k
2-n
2+3>0…①
设P(x
1,y
1),Q(x
2,y
2),则x
1+x
2=-
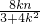
,x
1x
2=
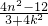
∵

∴x
1x
2+y
1y
2=0,即x
1x
2+(k
1x+n)(k
2x+n)=0,(1+k
2)x
1x
2+kn(x
1+x
2)+n
2=0
∴-
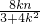
(1+k
2)+
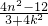
•kn+n
2=0,整理得12k
2=7n
2-12…②
①②联解,得n
2
,再由②知7n
2≥12,可得n≤-


或n≥


故直线l在y轴上截距的取值范围是(-∞,-


]∪[


,+∞)
(2)设直线l的方程为y=

x+n,与椭圆

+

=1消去y,得x
2+nx+n
2-3=0
可得根的判别式△=n
2-4(n
2-3)>0,化简得n
2<4…①
设P(x
1,y
1),Q(x
2,y
2),则x
1+x
2=-n,x
1x
2=n
2-3
∵

∴x
1x
2+y
1y
2=0,即x
1x
2+(

x+n)(

x+n)=0,

x
1x
2+

n(x
1+x
2)+n
2=0
∴

(n
2-3)+

n(-n)+n
2=0,整理得n
2=

…②
对照①②可得,n=±

所以存在直线l的方程:y=

x+

或y=

x-

,使得

.
分析:(1)根据题意,可得MN是线段PF
2的垂直平分线,所以点M的轨迹是以F
1、F
2为焦点的椭圆,结合题中数据不难得到轨迹C的方程;
(2)设直线l的方程为y=kx+n,与椭圆方程联解消去y,再结合根与系数的关系将

化为关于k、n的表达式,整理得12k
2=7n
2-12,最后用根的判别式建立不等式并解之,即可得到直线l在y轴上截距的取值范围;
(3)设直线l的方程为y=

x+n,与椭圆方程联解消去y,再结合根与系数的关系将

化为关于k、n的表达式,整理得n
2=

,结合根的判别式大于0,即可得n=±

,从而得到符合题意的直线l的方程.
点评:本题以向量的运算为载体,求曲线的轨迹方程,并且探索直线的存在性,着重考查了向量的数量积运算、求轨迹方程的一般方法和直线与椭圆的位置关系等知识,属于中档题.

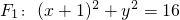 上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且
上任意一点,点F2的坐标为(1,0),直线m分别与线段F1P、F2P交于M、N两点,且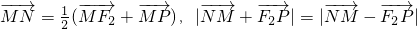 .
. (O为坐标原点).试求直线l在y轴上截距的取值范围;
(O为坐标原点).试求直线l在y轴上截距的取值范围; 的直线l与曲线C交于P、Q两点,使得
的直线l与曲线C交于P、Q两点,使得 (O为坐标原点),若存在求出直线l的方程,否则说明理由.
(O为坐标原点),若存在求出直线l的方程,否则说明理由.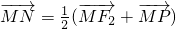 ,∴点N是线段PF2的中点
,∴点N是线段PF2的中点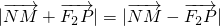 ,
,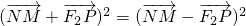 ,化简可得
,化简可得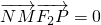
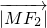 =
=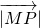 ,可得
,可得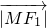 +
+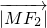 =
= =4
=4 +
+ =1,即为点M的轨迹C的方程;
=1,即为点M的轨迹C的方程; +
+ =1消去y,得(3+4k2)x2+8knx+4n2-12=0
=1消去y,得(3+4k2)x2+8knx+4n2-12=0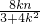 ,x1x2=
,x1x2=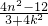

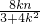 (1+k2)+
(1+k2)+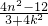 •kn+n2=0,整理得12k2=7n2-12…②
•kn+n2=0,整理得12k2=7n2-12…② ,再由②知7n2≥12,可得n≤-
,再由②知7n2≥12,可得n≤-
 或n≥
或n≥


 ]∪[
]∪[
 ,+∞)
,+∞) x+n,与椭圆
x+n,与椭圆 +
+ =1消去y,得x2+nx+n2-3=0
=1消去y,得x2+nx+n2-3=0
 x+n)(
x+n)( x+n)=0,
x+n)=0, x1x2+
x1x2+ n(x1+x2)+n2=0
n(x1+x2)+n2=0 (n2-3)+
(n2-3)+ n(-n)+n2=0,整理得n2=
n(-n)+n2=0,整理得n2= …②
…②
 x+
x+ 或y=
或y= x-
x- ,使得
,使得 .
. 化为关于k、n的表达式,整理得12k2=7n2-12,最后用根的判别式建立不等式并解之,即可得到直线l在y轴上截距的取值范围;
化为关于k、n的表达式,整理得12k2=7n2-12,最后用根的判别式建立不等式并解之,即可得到直线l在y轴上截距的取值范围; x+n,与椭圆方程联解消去y,再结合根与系数的关系将
x+n,与椭圆方程联解消去y,再结合根与系数的关系将 化为关于k、n的表达式,整理得n2=
化为关于k、n的表达式,整理得n2= ,结合根的判别式大于0,即可得n=±
,结合根的判别式大于0,即可得n=± ,从而得到符合题意的直线l的方程.
,从而得到符合题意的直线l的方程.

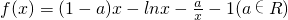
 时,设g(x)=x2-bx+1,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),求实数b的取值范围.
时,设g(x)=x2-bx+1,若对任意x1∈(0,2],都存在x2∈(0,2],都存在x2∈[1,2]使f(x1)≤g(x2),求实数b的取值范围.