
| A.4 | B.5 | C.6 | D.7 |
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:不详 题型:解答题
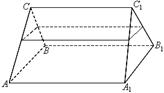
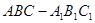 的各棱长均为2, 侧棱
的各棱长均为2, 侧棱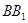 与底面
与底面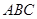 所成角为
所成角为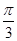 ,且侧面
,且侧面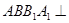 底面
底面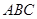 .
.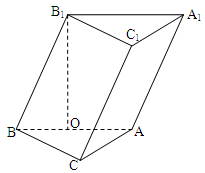
 (1)证明:点
(1)证明:点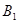 在平面
在平面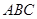 上的射影
上的射影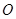 为
为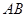 的中点;
的中点;


 (2)求二面角
(2)求二面角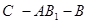 的大小;
的大小;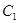 到平面
到平面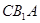 的距离.
的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
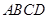 中,
中,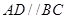 ,
,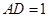 ,
,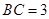 ,
,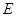 为
为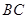 上一点,
上一点, 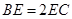 ,且
,且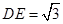 .将梯形
.将梯形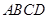 沿
沿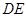 折成直二面角
折成直二面角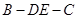 ,如图2所示.
,如图2所示.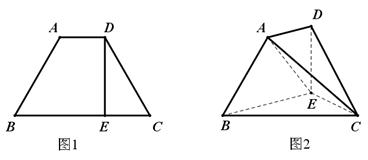
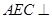 平面
平面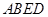 ;
;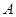 关于点
关于点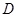 的对称点为
的对称点为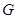 ,点
,点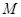 在
在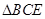 所在平面内,且直线
所在平面内,且直线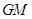 与平面
与平面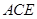 所成的角为
所成的角为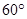 ,试求出点
,试求出点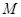 到点
到点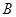 的最短距离.
的最短距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
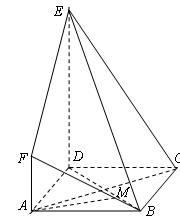
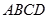 是边长为
是边长为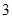 的正方形,
的正方形,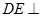 平面
平面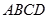 ,
,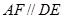 ,
,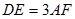 ,
,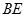 与平面
与平面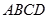 所成角为
所成角为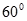 .
.
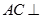 平面
平面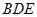 ;
;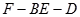 的余弦值;
的余弦值;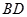 上是否存在点
上是否存在点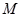 ,使得
,使得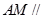 平面
平面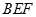 ?若存在,试确定点
?若存在,试确定点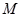 的位置;若不存在,说明理由。
的位置;若不存在,说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
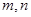 是两条不同的直线,
是两条不同的直线,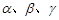 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题: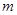 ⊥
⊥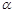 ,
, 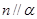 ,则
,则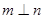 ;
;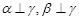 ,则
,则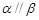 ;
;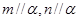 ,则
,则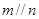 ;
;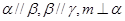 ,则
,则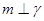 .
.| A.①和② | B.②和③ | C.③和④ | D.①和④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com