
分析 根据空间的一组基底满足的条件:不共面及零向量与任意向量关系的性质,判断出前者成立推不出后者成立;后者成立推出前者成立,利用充要条件的有关定义得到结论.
解答 解:$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$是三个非零向量成立,当$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$三个向量共面时,则{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}不为空间的一组基底,
即命题p推不出命题q;
但反之{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}为空间的一组基底,则$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$不共面,
所以$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是三个非零向量,
即命题q推出命题p;
所以命题q是命题p的充分不必要条件.
故答案为:充分不必要.
点评 解决一个命题是另一个命题的什么条件,应该先确定哪一个是条件,再两边试着双推一下,利用充要条件的有关定义下结论.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
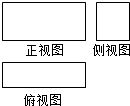 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在正视图中的投影长度为$\sqrt{6}$,在侧视图中的投影长度为$\sqrt{5}$,则该长方体的全面积为( )| A. | 3$\sqrt{5}$+2 | B. | 6$\sqrt{5}$+4 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-5=0 | B. | x-2y=0 | C. | 2x+y-3=0 | D. | x+2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com