
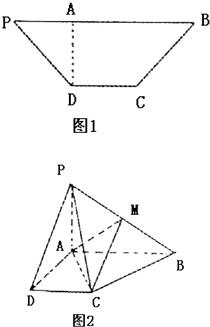
 已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=| 2 |
| 1 |
| 2 |
| AQ |
| AQ |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
| AQ |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AQ |
| AM |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| h |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| h |
| 3 |
| ||||
|
| 1 |
| 2 |
| 1 |
| 2 |
| AQ |
| 1 |
| 2 |
| 1 |
| 2 |
| AQ |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| 1 |
| 2 |
| AQ |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AQ |
| AM |


科目:高中数学 来源: 题型:
 已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=2a=|
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=2a=|| QP |
| QP′ |
(
|
(
|
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知等腰梯形PDCB中,PB=3,DC=1,PD=
已知等腰梯形PDCB中,PB=3,DC=1,PD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•盐城一模)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=
(2008•盐城一模)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年莱西一中模拟理)(12分)
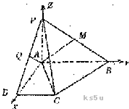
已知等腰梯形PDCB中(如图1),PB=3,DC=1,PD=BC=![]() ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面
PAD⊥面ABCD(如图2)。
(Ⅰ)证明:平面PAD⊥PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分![]() ;
;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线AM是否平行面PCD.
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com