
 .
.
 ,∴a=3
,∴a=3 ,0),
,0), ,
,
 ,
,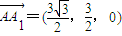

 =(x,y,1),则由
=(x,y,1),则由
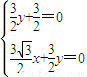 ,∴
,∴ ,∴
,∴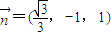
 =
=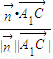 =-
=-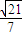
 与
与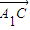 所成锐角互余,
所成锐角互余,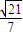 .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
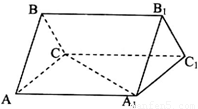
 如图三棱柱ABC-A1B1C1中,侧棱BB1与底面成60.角,AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P,且A1Q⊥B1C1,AB=AC,AQ=3,AP=2则顶点A到棱B1C1的距离是
如图三棱柱ABC-A1B1C1中,侧棱BB1与底面成60.角,AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P,且A1Q⊥B1C1,AB=AC,AQ=3,AP=2则顶点A到棱B1C1的距离是查看答案和解析>>
科目:高中数学 来源: 题型:
 如图三棱柱ABC-A1B1C1中,E,F分别是AB、AC的中点,平面EFC1B1将三棱柱分成体积为V1,V2(左为V1,右为V2)两部分,则V1:V2=( )
如图三棱柱ABC-A1B1C1中,E,F分别是AB、AC的中点,平面EFC1B1将三棱柱分成体积为V1,V2(左为V1,右为V2)两部分,则V1:V2=( )| A、7:5 | B、4:3 | C、3:1 | D、2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )查看答案和解析>>
科目:高中数学 来源: 题型:044
如图三棱柱ABC-A¢B¢C¢底面ABC是边长为a的正三角形,侧面ABB¢A¢是菱形,且ÐA¢AB=60°,M是A¢B¢中点,已知BM^AC.
(1)求证:BM^平面ABC;
(2)证明:平面ABB¢A¢^平面ABC;
(3)求异面直线AA¢和BC所成角的大小.
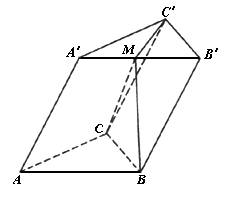
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)求证:BM^平面ABC;
(2)证明:平面ABB¢A¢^平面ABC;
(3)求异面直线AA¢和BC所成角的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com