
 如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )
如图,在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,B、C在平面α的同侧,M为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的△AB′C′,则AM与平面α所成角的正弦值的取值范围是( )| A. | [$\frac{\sqrt{42}}{7}$,1) | B. | [$\frac{\sqrt{42}}{7}$,1] | C. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$] | D. | [$\frac{\sqrt{42}}{7}$,$\frac{\sqrt{14}}{4}$) |
分析 推导出线段AM=$\frac{\sqrt{14}}{2}$,设B,C到平面α距离分别为a,b,则M到平面α距离为h=$\frac{a+b}{2}$,推导出ab=3,sinα=$\frac{h}{AM}$=$\frac{a+b}{\sqrt{14}}$,由此能求出AM与平面α所成角的正弦值的取值范围.
解答 解: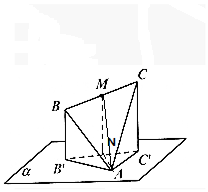 ∵在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,
∵在△ABC中,AB=AC=2,BC=$\sqrt{2}$,且A在平面α上,
B、C在平面α的同侧,M为BC的中点,
∴线段AM=$\sqrt{4-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{14}}{2}$
设B,C到平面α距离分别为a,b,
则M到平面α距离为h=$\frac{a+b}{2}$,
射影三角形两直角边的平方分别为4-a2,4-b2,
设线段BC射影长为c,则4-a2+4-b2=c2,
又线段AM射影长为$\frac{c}{2}$,①
∴($\frac{c}{2}$)2+($\frac{a+b}{2}$)2=AM2=$\frac{7}{2}$,②
由①②联立解得 ab=3,
所以sinα=$\frac{h}{AM}$=$\frac{a+b}{\sqrt{14}}$≥$\frac{2\sqrt{ab}}{\sqrt{14}}$=$\frac{2\sqrt{3}}{\sqrt{14}}$=$\frac{\sqrt{42}}{7}$,
当a=b=$\frac{3}{2}$时等号成立.
当面ABC与面α垂直时,sinα=1.
故选:B.
点评 本题考查线面角的正弦值的取值范围的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin$\frac{1}{2}$<cos$\frac{1}{2}$<tan$\frac{1}{2}$ | B. | cos$\frac{1}{2}$<sin$\frac{1}{2}$<tan$\frac{1}{2}$ | ||
| C. | sin$\frac{1}{2}$<tan$\frac{1}{2}$<cos$\frac{1}{2}$ | D. | tan$\frac{1}{2}$<sin$\frac{1}{2}$<cos$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>b,则ac>bc”是真命题 | |
| B. | 命题“若a2+b2=0,则a,b全为0”是真命题 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 命题“若a=0,则ab=0”的逆否命题是“若ab≠0,则a≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△A′DE,使得点A′在平面EBCD上的投影在CD上,且直线A′D与平面EBCD所成角为45°,则线段AE的长为2$\sqrt{2}$.
如图,已知矩形ABCD,AD=2,E为AB边上的点,现将△ADE沿DE翻折至△A′DE,使得点A′在平面EBCD上的投影在CD上,且直线A′D与平面EBCD所成角为45°,则线段AE的长为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com