
【题目】下列有关命题的说法正确的是__________________.
①命题“若x2-3x+2=0,则x=1”的逆否命题为:若x≠1,则x2-3x+2≠0
②x=1是x2-3x+2=0的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:x∈R,使得x2+x+1<0,则非p:x∈R, 均有x2+x+1≥0
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCED中,BE⊥CD,平面ABED⊥平面BCE.在梯形ABED中,AB∥DE,BE⊥AB.DE=BE=CE=2AB,M是BC的中点,点N在线段DE上,且满足DN=![]() DE.
DE.

(1)求证:MN∥平面ACD;
(2)若AB=2,求点N到平面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(-1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的菱形![]() 中,已知
中,已知![]() ,且
,且![]() .将梯形
.将梯形![]() 沿直线
沿直线![]() 折起,使
折起,使![]() 平面
平面![]() ,如图2,
,如图2,![]() 分别是
分别是![]() 上的点.
上的点.

(1)求证:图2中,平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)将红色卡片和蓝色卡片分别放在两个袋中,然后从两个袋中各取一张卡片,求两张卡片数字之积为偶数的概率
(2)将五张卡片放在一个袋子中,从中任取两张,求两张卡片颜色不同的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意
),对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为指数数列.
为指数数列.
(1)已知数列![]() 、
、![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 是不是指数数列(需说明理由);
是不是指数数列(需说明理由);
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 是指数数列;
是指数数列;
(3)若![]() 是指数数列,
是指数数列,![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
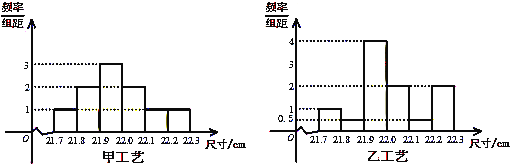
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com