
����Ŀ����ͼ������ƽ��ֱ������ϵxOy��x���ڵ�ƽ���ϣ�y�ᴹֱ�ڵ�ƽ�棬��λ����Ϊ1ǧ�ף�ij��λ������ԭ�㣮��֪�ڵ������Ĺ켣�ڷ���y=kx-![]() ��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
��ʾ�������ϣ�����k�뷢�䷽���йأ��ڵ������ָ�ڵ���ص�ĺ����꣮
��1����k=2ʱ�����ڵ���̣�
��2�����ڵ������̣�
��3�����ڵ�һ������һ������������С��������и߶�Ϊ3.2ǧ�ף��������ĺ�����a����������ʱ���ڵ���������������˵�����ɣ�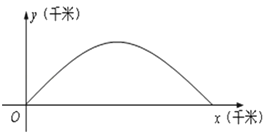
���𰸡��⣺��1����k=2��y=kx-![]() ���ɵã�y=2x-
���ɵã�y=2x-![]() ��y=0���ɵ�x=0��x=8��
��y=0���ɵ�x=0��x=8��
�ڵ����Ϊ��8ǧ�ף�
��2���� y=kx��![]() ��1+k2��x2��k��0������y=0���� kx��
��1+k2��x2��k��0������y=0���� kx��![]() ��1+k2��x2=0��
��1+k2��x2=0��
��ʵ���������������֪x��0��k��0��
��x=![]() =
=![]() ��
��![]() =10�����ҽ���k=1ʱȡ�Ⱥţ�
=10�����ҽ���k=1ʱȡ�Ⱥţ�
���ڵ���������10ǧ�ף�
��3����a��0�����ڵ����Ի���Ŀ��ȼ��ڴ��� k��0��ʹka��![]() ��1+k2��a2��3.2������
��1+k2��a2��3.2������
������k�ķ���a2k2��20ak+a2+64=0��������
��Τ�ﶨ����������֮�ʹ���0������֮������0��
��ֻ���=400a2��4a2��a2+64����0����a��6��
��ʱ��k=![]() ��0��
��0��
�൱a������6ʱ���ڵ����Ի���Ŀ�꣮
����������1��ͨ��k=2������������ʽ�������ö��κ��������̣�
��2�����ڵ�����Ŀ��ʱ�ĺ���������ֵ����һԪ���η��̸����б�ʽ��⼴�ɣ�
��3���ڵ����Ի���Ŀ��ȼ��ڴ��� k��0��ʹka��![]() ��1+k2��a2��3.2������ת��Ϊ����k�ķ���a2k2��20ak+a2+64=0�������������б�ʽ����⼴�ɣ�
��1+k2��a2��3.2������ת��Ϊ����k�ķ���a2k2��20ak+a2+64=0�������������б�ʽ����⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
�� ![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() ��
�� ![]() �����ҽ��㣬��
�����ҽ��㣬��![]() ����Բ
����Բ![]() ��.
��.
������![]() ����Сֵ��
����Сֵ��
������ֱ��![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
�� ![]() ���㣬����
���㣬����![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ����
����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��
��I��������![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��II����![]() ���������
���������![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У���
�У���![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ����ֱ��
���������Ϊ���Ὠ��������ϵ����ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��������
��������![]() �����е�ĺ���������Ϊԭ����һ�룬�����겻�䣬Ȼ��������ƽ��һ����λ�õ�����
�����е�ĺ���������Ϊԭ����һ�룬�����겻�䣬Ȼ��������ƽ��һ����λ�õ�����![]() ��
��
����������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������ֱ֪��![]() ������
������![]() ����
����![]() ���㣬��
���㣬��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ���ı���![]() ���������������Ϊ
���������������Ϊ![]() ��
�� ![]() ��
�� ![]() .
.
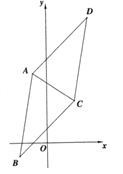
��1����ƽ���ı���![]() �Ķ���
�Ķ���![]() �����ꣻ
�����ꣻ
��2����![]() ����
�У���![]() ���ϵĸ�����ֱ�߷��̣�
���ϵĸ�����ֱ�߷��̣�
��3�����ı���![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ������
��Բ������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��Բ
��Բ![]() �ص��ҳ�Ϊ
�ص��ҳ�Ϊ![]() ��
��
������Բ![]() �ķ��̣�
�ķ��̣�
����Բ![]() ��һ��
��һ��![]() ��Բ�����ߣ������߷��̡�
��Բ�����ߣ������߷��̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����ΪR�ϵ��溯������x��0ʱ��f��x��=x2+2x��
��1����f��x���Ľ���ʽ��
��2��������ʽf��t��2��+f��2t+1����0��������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ��
��1����֪loga ![]() ��1����a��
��1����a�� ![]() ��
��
��2������y=2x��ͼ���뺯��y=2��x��ͼ�����y��Գƣ�
��3������f��x��=lg��mx2+mx+1���Ķ�������R����m��ȡֵ��Χ��0��m��4��
��4������y=ln����x2+x���ĵ�������Ϊ�����ޣ� ![]() ]
]
��ȷ���� �� ��������Ϊ��ȷ�����ȫ��д�ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x��=ax2+bx+c��a��0������f[2]��x��=f��f��x����������f��x��=x2+1��
��f[2]��x��=��f��x����2+1=��x2+1��2+1��
��1��f��x��=x2��x�������x�ķ���f[2]��x��=x��
��2���ǡ�=��b��1��2��4ac����f[2]��x��=x���ĸ�����ȵ�ʵ�����������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com