
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() △
△![]() 为等边三角形,
为等边三角形, ![]() 是
是![]() 上的点,且
上的点,且![]() .
.
(1)求![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?说明理由.
?说明理由.
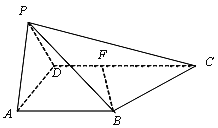
【答案】(1)![]() (2)PB中点
(2)PB中点
【解析】试题分析:(1)分别利用等腰三角形的三线合一和线面垂直的性质得到线线垂直,进而利用线面垂直的判定定理证明线面垂直,作出线面角,再利用直角三角形进行求解;(2)先猜出该点位置,再利用利用线面垂直的判定定理进行证明.
试题解析:(1)取AD中点H,PD=PA, 所以![]() ,因为AB
,因为AB![]() 平面PAD,且PH
平面PAD,且PH![]() 平面PAD,
平面PAD,
所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() ∠PCH是PC和平面ABCD所成的角.
∠PCH是PC和平面ABCD所成的角.
不妨令AB=2 ,CH=![]()
在△![]()
(2)线段![]() 上存在点
上存在点![]() ,使
,使![]() 平面
平面![]() .
.
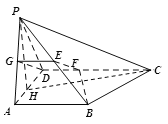
理由如下:如图,分别取![]() 的中点G、E,则
的中点G、E,则![]() , 由
, 由![]() , 所以
, 所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,故
为平行四边形,故![]() .
.
因为AB![]() 平面PAD,所以
平面PAD,所以![]() ,因此,
,因此, ![]() ,因为
,因为![]() 为
为![]() 的中点,且
的中点,且![]() ,
, ![]() ,因此
,因此![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
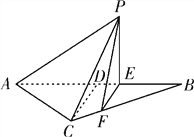
【题目】如图所示,等腰![]() 的底边
的底边![]() ,高
,高![]() ,点
,点![]() 是线段
是线段![]() 上异于点
上异于点![]() 的动点,点
的动点,点![]() 在
在![]() 边上,且
边上,且![]() ,现沿
,现沿![]() 将△
将△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,记
,记![]() ,
, ![]() 表示四棱锥
表示四棱锥![]() 的体积.
的体积.
(1)求![]() 的表达式;(2)当
的表达式;(2)当![]() 为何值时,
为何值时, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
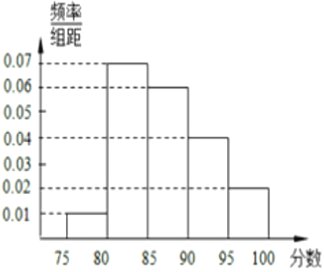
【题目】某高校在今年的自主招生考试成绩中随机抽取 100 名考生的笔试成绩,分为 5 组制出频率分布直方图如图所示.
组号 | 分组 | 频数 | 频率 |
1 |
| 5 | 0.05 |
2 |
| 35 | 0.35 |
3 |
|
|
|
4 |
|
|
|
5 |
| 10 | 0.1 |
(1)求![]() 的值.
的值.
(2)该校决定在成绩较好的 、4、5 组用分层抽样抽取 6 名学生进行面试,则每组应各抽多少名学生?
(3)在(2)的前提下,从抽到 6 名学生中再随机抽取 2 名被甲考官面试,求这 2 名学生来自同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com