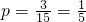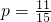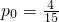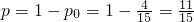一个袋装着标有数字1,2,3,4,5,6的小球各一个,从袋中任取2个小球,并且每个小球被取出的可能性相等,按2个小球上的数字之和计分.
(1)用“列举法”计算“2个小球上数字之和为7分”的概率;
(2)求得分不少于6的概率.
解:(1)从六个小球中任取2个,所有可能的基本事件:
(1,2)(1,3)(1,4)(1,5)(1,6)
(2,3)(2,4)(2,5)(2,6)
(3,4)(3,5)(3,6)
(4,5)(4,6)
(5,6)
共15个基本事件
事件“2个小球上数字之和为7分”有:(1,6)(2,5)(3,4)共3个基本事件
∴“2个小球上数字之和为7分”的概率为:
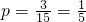
(2)方法一:得分不少于6分共有:(1,5)(1,6)(2,4)(2,5)(2,6)(3,4)(3,5)(3,6)(4,5)(4,6)(5,6)11个基本事件
∴得分不少于6分的概率为:
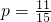
方法二:得分少于6分共有:(1,2)(1,3)(1,4)(2,3)
∴所以得分少于6分的概率为:
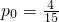
∴得分不少于6分的概率为:
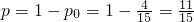
分析:(1)列出所有可能的基本事件,列出事件“2个小球上数字之和为7分”所含的基本事件,两者个数比即为所求概率
(2)方法一:事件“得分不小于6”所包含的基本事件数与所有可能的基本事件的个数比即为所求
方法二:先求“得分小于6”的对立事件的概率p
0,则1-p
0即为所求
点评:本题考查古典概型,用列举法求事件的概率,列举时一定要按照一定的规律列举,以免重复或遗漏,属简单题