练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=x2﹣2|x|．

    （1）将函数f（x）写成分段函数；

    （2）判断函数的奇偶性，并画出函数图象．

    （3）若函数在[a, +∞)上单调，求a的范围。

    【答案】（1）（2）见解析（3）

    【解析】试题分析：（1）对自变量分类讨论，得到分段函数；（2）确定函数的定义域，验证f（﹣x）与f（x）的关系，可得函数的奇偶性；利用配方法确定函数的对称轴与顶点坐标，即可得到函数的图象；（3）由（2）图象可得：a的范围.

    试题解析：

    (1)当x＞0时，f（x）=x2﹣2x．

    当x=0时，f（x）=0．

    当x<0时，f（x）=x2+2x．

    ∴函数f（x）在R上的解析式为

    ，

    (2)f(x)的定义域为R

    f(-x)=(-x2)-2|-x|=f(x)

    ∴f（x）是偶函数，

    图象如图

    （3）∵函数在[a, +∞)上单调，

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x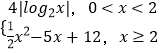）= ，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（ ）
    A.（16，21）
    B.（16，24）
    C.（17，21）
    D.（18，24）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】综合题。
    （1）四个不同球放入编号为1，2，3，4的四个盒中，则恰有一个空盒的放法有多少种？
    （2）设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的盒子现将这5个球投入5个盒子要求每个盒子放一个球，并且恰好有两个球的号码与盒子号码相同，问有多少种不同的方法？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

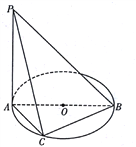
    【题目】如图， 是直径， 所在的平面， 是圆周上不同于的动点.

    （1）证明：平面平面；

    （2）若，且当二面角的正切值为时，求直线与平面所成的角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某球星在三分球大赛中命中率为 ，假设三分球大赛中总计投出8球，投中一球得3分，投丢一球扣一分，则该球星得分的期望与方差分别为（ ）
    A.16，32
    B.8，32
    C.8，8
    D.32，32

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线C极坐标方程： ，点P极坐标为 ，直线l过点P，且倾斜角为 ．
    （1）求曲线C的直角坐标方程及直线l参数方程；
    （2）若直线l与曲线C交于A，B两点，求 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点A(m－1,2)，B(1,1)，C(3，m2－m－1)．

    (1)若A，B，C三点共线，求实数m的值；

    (2)若AB⊥BC，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .
    （1）若曲线 在点 处的切线斜率为3，且 时 有极值，求函数 的解析式；
    （2）在（1）的条件下，求函数 在 上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】( 本小题满分14)

    如图，在三棱锥P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．

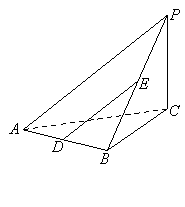
    (1)求证：DE∥平面PAC

    (2)求证：AB⊥PB

    查看答案和解析>>

    同步练习册答案