
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°. 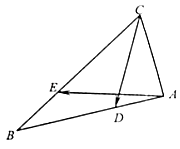
(1)求| ![]() |;
|;
(2)已知点D是AB上一点,满足 ![]() =λ
=λ ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足 ![]() =λ
=λ ![]() . ①当λ=
. ①当λ= ![]() 时,求
时,求 ![]()
![]() ;
;
②是否存在非零实数λ,使得 ![]() ⊥
⊥ ![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
【答案】
(1)解:△ABC中,CA=1,CB=2,∠ACB=60°,
由余弦定理得,
AB2=CA2+CB2﹣2CACBcos∠ACB
=12+22﹣2×1×2×cos60°
=3,
∴AB= ![]() ,即|
,即| ![]() |=
|= ![]() ;
;
(2)解:①λ= ![]() 时,
时, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴D、E分别是BC,AB的中点,
∴ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ,
,
![]() =
= ![]() (
( ![]() +
+ ![]() ),
),
∴ ![]()
![]() =(
=( ![]() +
+ ![]() )
) ![]() (
( ![]() +
+ ![]() )
)
= ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
=﹣ ![]() ×12+
×12+ ![]() ×1×2×cos120°+
×1×2×cos120°+ ![]() ×2×1×cos60°+
×2×1×cos60°+ ![]() ×22
×22
= ![]() ;
;
②假设存在非零实数λ,使得 ![]() ⊥
⊥ ![]() ,
,
由 ![]() =λ
=λ ![]() ,得
,得 ![]() =λ(
=λ( ![]() ﹣
﹣ ![]() ),
),
∴ ![]() =
= ![]() +
+ ![]() =
= ![]() +λ(
+λ( ![]() ﹣
﹣ ![]() )=λ
)=λ ![]() +(1﹣λ)
+(1﹣λ) ![]() ;
;
又 ![]() =λ
=λ ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() =(
=( ![]() ﹣
﹣ ![]() )+λ(﹣
)+λ(﹣ ![]() )=(1﹣λ)
)=(1﹣λ) ![]() ﹣
﹣ ![]() ;
;
∴ ![]()
![]() =λ(1﹣λ)
=λ(1﹣λ) ![]() ﹣λ
﹣λ ![]()
![]() +(1﹣λ)2
+(1﹣λ)2![]()
![]() ﹣(1﹣λ)
﹣(1﹣λ) ![]()
=4λ(1﹣λ)﹣λ+(1﹣λ)2﹣(1﹣λ)
=﹣3λ2+2λ=0,
解得λ= ![]() 或λ=0(不合题意,舍去);
或λ=0(不合题意,舍去);
即存在非零实数λ= ![]() ,使得
,使得 ![]() ⊥
⊥ ![]() .
.
【解析】(1)利用余弦定理求出AB的长即得| ![]() |;(2)①λ=
|;(2)①λ= ![]() 时,D、E分别是BC,AB的中点,求出
时,D、E分别是BC,AB的中点,求出 ![]() 、
、 ![]() 的数量积即可;②假设存在非零实数λ,使得
的数量积即可;②假设存在非零实数λ,使得 ![]() ⊥
⊥ ![]() ,利用
,利用 ![]() 、
、 ![]() 分别表示出
分别表示出 ![]() 和
和 ![]() ,
,
求出 ![]()
![]() =0时的λ值即可.
=0时的λ值即可.


科目:高中数学 来源: 题型:
【题目】已知全集U为R,集合A={x|x2<4},B= ![]() (x﹣2)},则下列关系正确的是( )
(x﹣2)},则下列关系正确的是( )
A.A∪B=R
B.A∪(∪B)=R
C.(∪A)∪B=R
D.A∩(∪B)=A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(a﹣2)x﹣2,a∈R.
(1)若关于x的不等式f(x)≤0的解集为[﹣1,2],求实数a的值;
(2)当a<0时,解关于x的不等式f(x)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最下正周期为π,且点P(
)的最下正周期为π,且点P( ![]() ,2)是该函数图象的一个人最高点.
,2)是该函数图象的一个人最高点.
(1)求函数f(x)的解析式;
(2)若x∈[﹣ ![]() ,0],求函数y=f(x)的值域;
,0],求函数y=f(x)的值域;
(3)把函数y=f(x)的图线向右平移θ(0<θ< ![]() )个单位,得到函数y=g(x)在[0,
)个单位,得到函数y=g(x)在[0, ![]() ]上是单调增函数,求θ的取值范围.
]上是单调增函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市交通局为了解机动车驾驶员对交通法规的知晓情况,对渤海、丰乐、安宁、天正四个社区做分层抽样调查.其中渤海社区有驾驶员96人.若在渤海、丰乐、安宁、天正四个社区抽取驾驶员的人数分别为12,21,25,43,则丰乐、安宁、天正三个社区驾驶员人数是多少( )
A.101
B.808
C.712
D.89
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知向量 ![]() ,
, ![]() ,定点
,定点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 满足
满足 ![]() ,曲线
,曲线 ![]() ,区域
,区域 ![]() ,曲线
,曲线 ![]() 与区域
与区域 ![]() 的交集为两段分离的曲线,则( )
的交集为两段分离的曲线,则( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如表所示:
根据下表信息解答以下问题:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
(1)从该单位任选两名职工,用η表示这两人休年假次数之和,记“函数f(x)=x2﹣ηx﹣1在区间(4,6)上有且只有一个零点”为事件A,求事件A发生的概率P;
(2)从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C. 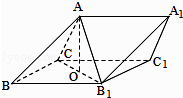
(1)证明:B1C⊥AB;
(2)若AC⊥AB1 , ∠CBB1=60°,BC=1,求三棱柱ABC﹣A1B1C1的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com