练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(1)已知函数f(x)的定义域为[0,1]，求f(x2＋1)的定义域；

    (2)已知f()的定义域为[0,3]，求f(x)的定义域．

    【答案】(1) {0};(2) [1,2].

    【解析】试题分析:(1) 函数f(x2＋1)中的x2＋1相当于函数f(x)中的x，∴0≤x2＋1≤1，解出x的取值范围,即f(x2＋1)的定义域；(2) f()的定义域为[0,3]，即0≤x≤3,由此可求出的范围,即f(x)的定义域．

    试题解析:

    (1)∵函数f(x2＋1)中的x2＋1相当于函数f(x)中的x，∴0≤x2＋1≤1，∴－1≤x2≤0，∴x＝0，

    ∴f(x2＋1)的定义域为{0}．

    (2)∵f()的定义域为[0,3]，∴0≤x≤3，∴1≤≤2，∴f(x)的定义域为[1,2]．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（, 是自然对数的底数）.

    （1）当时，求曲线在点处的切线方程；

    （2）当时，不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在各项都不相等的等差数列{an}中，a1，a2是关于x的方程x2－7a4x＋18a3＝0的两个实根．

    (1) 试判断－22是否在数列{an}中；

    (2) 求数列{an}的前n项和Sn的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义区间(a,b)，[a,b)，(a,b]，[a,b]的长度均为，多个区间并集的长度为各区间长度之和，例如,(1,2) [3,5)的长度d=(2-1)+(5-3)=3. 用[x]表示不超过x的最大整数，记{x}=x-[x]，其中.设， ，当时,不等式解集区间的长度为，则的值为_______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中

    （1）当时，求函数在处的切线方程；

    （2）若函数在定义域上有且只有一个极值点，求实数的取值范围；

    （3）若对任意恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.

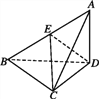
    (1)求证:平面ABC⊥平面ACD;

    (2)若E为AB中点,求点A到平面CED的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的两个焦点分别为，离心率为.设过点的直线与椭圆相交于不同两点， 周长为.

    （Ⅰ）求椭圆C的标准方程；

    （Ⅱ）已知点，证明：当直线变化时，总有TA与的斜率之和为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

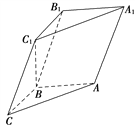
    【题目】如图，在三棱柱ABCA1B1C1中，已知AB⊥侧面BB1C1C，AB＝BC＝1，BB1＝2，∠BCC1＝ .

    (1)求证：C1B⊥平面ABC；

    设 (0≤λ≤1)，且平面AB1E与BB1E所成的锐二面角的大小为30°，

    试求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某综艺节目为增强娱乐性，要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会；凡是选择表演节目的好友均需连线未参加过此活动的个好友参与此活动，以此下去.

    （Ⅰ）假设每个人选择表演与否是等可能的，且互不影响，则某人选择表演后，其连线的个好友中不少于个好友选择表演节目的概率是多少？

    （Ⅱ）为调查“选择表演者”与其性别是否有关，采取随机抽样得到如下列表：

    选择表演

    拒绝表演

    合计

    男

    50

    10

    60

    女

    10

    10

    20

    合计

    60

    20

    80

    ①根据表中数据，是否有的把握认为“表演节目”与好友的性别有关？

    ②将此样本的频率视为总体的概率，随机调查名男性好友，设为个人中选择表演的人数，求的分布列和期望.

    附：；

    0.15

    0.10

    0.05

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    同步练习册答案