
【题目】如图,矩形![]() 所在平面与等边
所在平面与等边![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
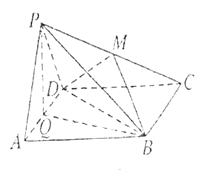
(1)求证:![]() 平面
平面![]() .
.
(2)试问:在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试指出点
?若存在,试指出点![]() 的位置,并证明你的结论:若不存在,请说明理由.
的位置,并证明你的结论:若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
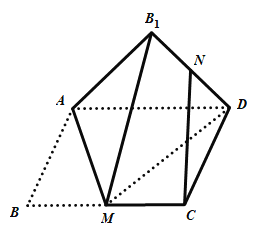
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,
,![]() 且椭圆上存在一点P,满足.
且椭圆上存在一点P,满足.![]() ,
,![]()
(1)求椭圆C的标准方程;
(2)已知A,B分别是椭圆C的左、右顶点,过![]() 的直线交椭圆C于M,N两点,记直线
的直线交椭圆C于M,N两点,记直线![]() ,
,![]() 的交点为T,是否存在一条定直线l,使点T恒在直线l上?
的交点为T,是否存在一条定直线l,使点T恒在直线l上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
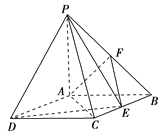
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 与平面
与平面![]() 所成角的大小为45°.
所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 是半圆
是半圆![]() 上除点
上除点![]() 外的一个动点,
外的一个动点,![]() 垂直于
垂直于![]() 所在的平面,垂足为
所在的平面,垂足为![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 为半圆弧的中点时,求二面角
为半圆弧的中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,逦过分层抽样获得12名员工每天睡眠的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | ||
乙部门 | 6 | 6.5 | 7 | 7.5 | |
丙部门 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数;
(2)若将每天睡眠时间不少于7小时视为睡眠充足,现从该单位任抽取1人,估计抽到的此人为睡眠充足者的概率;
(3)从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B.假设所有员工睡眠的时间相互独立.求A的睡眠时间不少于B的睡眠时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 由an与Sn的关系求通项公式
(1)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)已知正项数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).求数列
).求数列![]() 的通项公式;
的通项公式;
(3)已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,求Sn
(4)已知正项数列![]() 中,
中,![]() ,
,![]() ,前n项和为
,前n项和为![]() ,且满足
,且满足![]() (
(![]() ).求数列
).求数列![]() 的通项公式;
的通项公式;
(5)设数列{an}的前n项积为Tn,且Tn+2an=2(n∈N*).数列![]() 是等差数列;求数列
是等差数列;求数列![]() 的通项公式;
的通项公式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com