
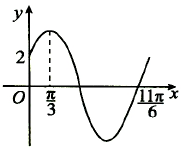
 已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.分析 (1)由函数f(x)的部分图象,求出最小正周期T得ω;由f($\frac{π}{3}$)=A求出φ,由f(0)=2求出A即得f(x)解析式;
(2)化函数y为正弦型函数,求出$x∈[{-\frac{π}{2},\frac{π}{12}}]$时函数y的最大、最小值即可.
解答 解:(1)由函数f(x)=Asin(ωx+φ)的部分图象知,
$\frac{3}{4}$T=$\frac{11π}{6}$-$\frac{π}{3}$=$\frac{3π}{2}$,
∴T=2π,
∴ω=$\frac{2π}{T}$=1;
又f($\frac{π}{3}$)=Asin($\frac{π}{3}$+φ)=A,且0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$;
∴f(0)=Asin$\frac{π}{6}$=2,
∴A=4;
∴f(x)=4sin(x+$\frac{π}{6}$);
(2)函数$y=f({x+\frac{π}{12}})-\sqrt{2}f({x+\frac{π}{3}})$
=4sin(x+$\frac{π}{12}$+$\frac{π}{6}$)-4$\sqrt{2}$sin(x+$\frac{π}{3}$+$\frac{π}{6}$)
=4sin(x+$\frac{π}{4}$)-4$\sqrt{2}$sin(x+$\frac{π}{2}$)
=4×$\frac{\sqrt{2}}{2}$sinx+4×$\frac{\sqrt{2}}{2}$cosx-4$\sqrt{2}$cosx
=2$\sqrt{2}$sinx-2$\sqrt{2}$cosx
=4sin(x-$\frac{π}{4}$);
当$x∈[{-\frac{π}{2},\frac{π}{12}}]$时,x-$\frac{π}{4}$∈[-$\frac{3π}{4}$,-$\frac{π}{6}$];
∴x-$\frac{π}{4}$=-$\frac{π}{2}$,即x=-$\frac{π}{4}$时,函数y取得最小值-4;
x-$\frac{π}{4}$=-$\frac{π}{6}$,即x=$\frac{π}{12}$时,函数y取得最大值-2.
点评 本题考查了正弦型函数的图象与性质的应用问题,也考查了三角恒等变换的应用问题,是综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高中以下 | 高中以上 | 合计 | |
| 支持 | 22 | 68 | 90 |
| 不支持 | 8 | 2 | 10 |
| 合计 | 30 | 70 | 100 |
| P(K2≤k) | 0.010 | 0.005 | 0.001 |
| k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | V=$\frac{1}{3}$abc(a,b,c,为底面边长) | |
| B. | V=$\frac{1}{3}$Sh(S为底面面积,h为四面体的高) | |
| C. | V=$\frac{1}{3}$(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面 体内切球的半径) | |
| D. | V=$\frac{1}{3}$(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$(4n-1) | B. | $\frac{1}{3}$(2n-1) | C. | 4n-1 | D. | $\frac{1}{3}$(4n+8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com