
【题目】如图所示,一个圆锥形的空杯子上放着一个直径为8cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?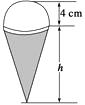
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上函数f(x)是可导的,f(1)=2,且f(x)+f'(x)<1,则不等式f(x)﹣1<e1﹣x的解集是( )(注:e为自然对数的底数)
A.(1,+∞)
B.(﹣∞,0)∪(0,1)
C.(0,1)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,直线l:y+x﹣t=0,P为直线l上一动点,O为坐标原点.
(1)若直线l交圆C于A、B两点,且∠AOB= ![]() ,求实数t的值;
,求实数t的值;
(2)若t=4,过点P做圆的切线,切点为T,求 ![]()
![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知 ![]() 是圆
是圆 ![]() 上一点,折叠该圆两次使点
上一点,折叠该圆两次使点 ![]() 分别与圆上不相同的两点(异于点
分别与圆上不相同的两点(异于点 ![]() )重合,两次的折痕方程分别为
)重合,两次的折痕方程分别为 ![]() 和
和 ![]() ,若圆
,若圆 ![]() 上存在点
上存在点 ![]() ,使
,使 ![]() ,其中
,其中 ![]() 的坐标分别为
的坐标分别为 ![]() ,则实数
,则实数 ![]() 的取值集合为 .
的取值集合为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,值域为
,值域为 ![]() ,如果存在函数
,如果存在函数 ![]() ,使得函数
,使得函数 ![]() 的值域仍是
的值域仍是 ![]() ,那么称
,那么称 ![]() 是函数
是函数 ![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数 ![]() 是不是函数
是不是函数 ![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
① ![]() ;
;
② ![]() .
.
(2)设 ![]() 的定义域为
的定义域为 ![]() ,已知
,已知 ![]() 是
是 ![]() 的一个等值域变换,且函数
的一个等值域变换,且函数 ![]() 的定义域为
的定义域为 ![]() ,求实数
,求实数 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞]上单调递增,若实数a满足f(log2a)+f( ![]() )≤2f(1),则a的取值范围是( )
)≤2f(1),则a的取值范围是( )
A.[1,2]
B.(0, ![]() ]
]
C.(0,2]
D.[ ![]() ,2]
,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a﹣ ![]() )x2+lnx(a为实数).
)x2+lnx(a为实数).
(1)当a=0时,求函数f(x)在区间[ ![]() ,e]上的最大值和最小值;
,e]上的最大值和最小值;
(2)若对任意的x∈(1,+∞),g(x)=f(x)﹣2ax<0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.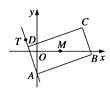
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com