
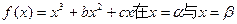 处有两上不同的极值点,设
处有两上不同的极值点,设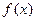 在点
在点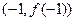 处切线为
处切线为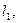 其斜率为
其斜率为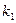 ;在点
;在点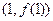 利的切线为
利的切线为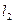 ,其斜率为
,其斜率为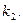
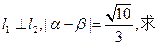
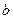 和
和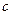 的值
的值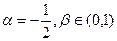 ,求
,求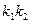 的取值范围。
的取值范围。科目:高中数学 来源:不详 题型:解答题
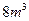 ,深为2m的长方体无盖水池,如果池底的造价为每平方米120元,池壁的造价为每平方米80元,求这个水池的最低造价
,深为2m的长方体无盖水池,如果池底的造价为每平方米120元,池壁的造价为每平方米80元,求这个水池的最低造价
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
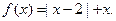
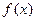 的值域;
的值域;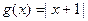 ,求
,求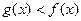 成立时
成立时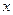 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
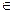 D,使得当x
D,使得当x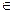 D且x>x0时,总有
D且x>x0时,总有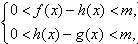 则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=
则称直线l:y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=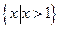 的四组函数如下:
的四组函数如下: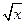 ; ②f(x)=10-x+2,g(x)=
; ②f(x)=10-x+2,g(x)= 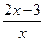 ;
;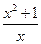 ,g(x)=
,g(x)= 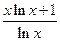 ; ④f(x)=
; ④f(x)= 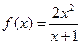 ,g(x)=2(x-1-e-x).
,g(x)=2(x-1-e-x).| A.①④ | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ①当a≥1时,不等式
①当a≥1时,不等式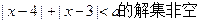
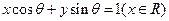 都相切
都相切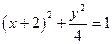 ,则
,则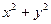 的取值范围是 [1,
的取值范围是 [1, 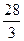 ]
]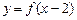 和
和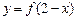 的图象关于直线
的图象关于直线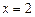 对称.
对称.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
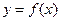 满足:
满足: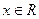 都有
都有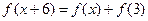 成立;
成立;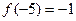 ;
;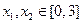 且
且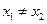 时,都有
时,都有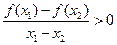 .
.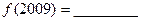 ;
;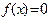 在区间
在区间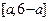 上恰有3个不同实根,则实数
上恰有3个不同实根,则实数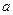 的取值范围是____.
的取值范围是____.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com