A
分析:p
1:先分别将sin15°+cos15°,sin16°+cos16°都化成关于不同角的正弦函数的形式,再利用三角函数的单调性即可比较它们的大小;
p
2:若一个三角形两内角α、β满足sinα•cosβ<0,说明一个角是钝角,即可判断正误;
P
3将根号中的式子利用二倍角公式化为平方形式,再注意正弦函数的符号即可判断正误.
p
4:要得到函数
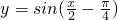
的图象,只需将函数
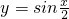
的图象向右平移

个单位.即可判断结论的正误;
解答:p
1:∵a=sin15°+cos15°=

sin(45°+15°)=

sin60°;
b=sin16°+cos16=

sin(45°+16°)=

sin61°;
又函数y=

sinx在(0°,90°)上是增函数,
∴

sin61°<

sin61°
sin15°+cos15°<sin16°+cos16°,
故P
1错误;
p
2:若一个三角形两内角α、β满足sinα•cosβ<0,所以cosβ<0,则此三角形为钝角三角形;正确.
P
3:?x∈[0,π],sinx>0,且1-cos2x=2sin
2x,所以
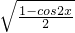
=sinx正确;
p
4:将函数
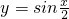
的图象向右平移

个单位.得到函数
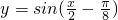
的图象,所以不正确.
综上知,p
1,p
4是假命题
故选A.
点评:本题是综合题,考查三角函数以及三角形的有关知识,考查知识的综合应用,属于基础题.

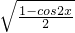 =sinx;p4:要得到函数
=sinx;p4:要得到函数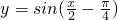 的图象,只需将函数
的图象,只需将函数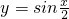 的图象向右平移
的图象向右平移 个单位.其中为假命题的是
个单位.其中为假命题的是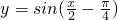 的图象,只需将函数
的图象,只需将函数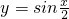 的图象向右平移
的图象向右平移 个单位.即可判断结论的正误;
个单位.即可判断结论的正误; sin(45°+15°)=
sin(45°+15°)= sin60°;
sin60°; sin(45°+16°)=
sin(45°+16°)= sin61°;
sin61°; sinx在(0°,90°)上是增函数,
sinx在(0°,90°)上是增函数, sin61°<
sin61°< sin61°
sin61°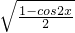 =sinx正确;
=sinx正确;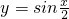 的图象向右平移
的图象向右平移 个单位.得到函数
个单位.得到函数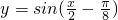 的图象,所以不正确.
的图象,所以不正确.
