
【题目】已知函数 ![]() .
.
(1)试判断f (x)的单调性,并证明你的结论;
(2)若f (x)为定义域上的奇函数,求函数f (x)的值域.
【答案】
(1)解:f (x)是增函数.
证明如下:函数f (x)的定义域为(﹣∞,+∞),且 ![]() ,
,
任取x1,x2∈(﹣∞,+∞),且x1<x2,
则 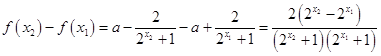 .
.
∵y=2x在R上单调递增,且x1<x2,
∴ ![]() ,
,
∴f (x2)﹣f (x1)>0,即f (x2)>f (x1),
∴f (x)在(﹣∞,+∞)上是单调增函数
(2)解:∵f (x)是定义域上的奇函数,∴f (﹣x)=﹣f (x),
即 ![]() 对任意实数x恒成立,化简得
对任意实数x恒成立,化简得 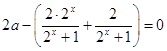 ,
,
∴2a﹣2=0,即a=1.(也可利用f (0)=0求得a=1)∴ ![]() ,
,
∵2x+1>1,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .
.
故函数f (x)的值域为(﹣1,1)
【解析】(1)f (x)是增函数,利用单调性的定义进行证明;(2)先求出a,再求函数f (x)的值域.
【考点精析】关于本题考查的函数单调性的判断方法和函数奇偶性的性质,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了调查“五一”小长假出游选择“有水的地方”是否与性别有关,现从该市“五一”出游旅客中随机抽取500人进行调查,得到如下2×2列联表:(单位:人)
选择“有水的地方” | 不选择“有水的地方” | 合计 | |
男 | 90 | 110 | 200 |
女 | 210 | 90 | 300 |
合计 | 300 | 200 | 500 |
(Ⅰ)据此样本,有多大的把握认为选择“有水的地方”与性别有关;
(Ⅱ)若以样本中各事件的频率作为概率估计全市“五一”所有出游旅客情况,现从该市的全体出游旅客(人数众多)中随机抽取3人,设3人中选择“有水的地方”的人数为随机变量X,求随机变量X的数学期望和方差.
附临界值表及参考公式:
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
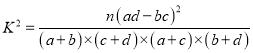 ,n=a+b+c+d.
,n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人.若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(Ⅰ)求表格中的数据![]() ;
;
(Ⅱ)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取30件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数分布表:
,得到如下的频数分布表:
|
|
|
|
|
频数 | 2 | 6 | 18 | 4 |
(I)估计该技术指标值的平均数和众数(以各组区间的中点值代表该组的取值);
(II) 若![]() 或
或![]() ,则该产品不合格,其余的是合格产品,从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于
,则该产品不合格,其余的是合格产品,从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于![]() 的产品恰有1件的概率.
的产品恰有1件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年入冬以来,各地雾霾天气频发, ![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
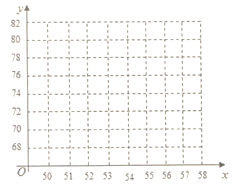
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式: 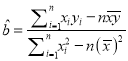
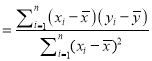 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com