
【题目】已知位置向量 ![]() =(log2(m2+3m﹣8),log2(2m﹣2)),
=(log2(m2+3m﹣8),log2(2m﹣2)), ![]() =(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y=
=(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y= ![]() x的图象上,则实数m= .
x的图象上,则实数m= .
【答案】2或5
【解析】解:以OA、OB为邻边的平行四边形OACB的顶点是C,则 ![]() =
= ![]() +
+ ![]() =(log2(m2+3m﹣8),log2(2m﹣2))+(1,0)=(1+log2(m2+3m﹣8),log2(2m﹣2))=(log2(2m2+6m﹣16),log2(2m﹣2)),
=(log2(m2+3m﹣8),log2(2m﹣2))+(1,0)=(1+log2(m2+3m﹣8),log2(2m﹣2))=(log2(2m2+6m﹣16),log2(2m﹣2)),
即C(log2(2m2+6m﹣16),log2(2m﹣2)),
∵顶点C在函数y= ![]() x的图象上,
x的图象上,
∴log2(2m﹣2)= ![]() log2(2m2+6m﹣16),
log2(2m2+6m﹣16),
即2log2(2m﹣2)=log2(2m2+6m﹣16),
即(2m﹣2)2=2m2+6m﹣16,
即m2﹣7m+10=0
得m=2或m=5,
检验知m=2或m=5满足条件,
所以答案是:2或5.


科目:高中数学 来源: 题型:
【题目】学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: 
(1)求该运动员得分的中位数和平均数;
(2)估计该运动员每场得分超过10分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
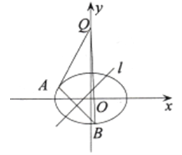
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某人的射击技术情况,在他的训练记录中抽取50次检验,他的命中环数如下:10,5,5,8,7,8,6,9,7,8,6,6,5,6,7,8,10,9,7,9,8,7,6,5,9,9,8,8,5,8,6,7,6,9,6,8,8,8,6,7,6,8,107,10,8,7,7,9,5
(1)列出频率分布表
(2)画出频率分布的直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣ ![]() )eax(a>0).
)eax(a>0).
(1)求函数y=f(x)的最小值;
(2)若存在唯一实数x0 , 使得f(x0)+ ![]() =0成立,求实数a的值.
=0成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为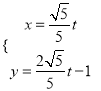 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com