
【题目】平面上两点A(﹣1,0),B(1,0),在圆C:(x﹣3)2+(y﹣4)2=4上取一点P,
(Ⅰ)x﹣y+c≥0恒成立,求c的范围
(Ⅱ)从x+y+1=0上的点向圆引切线,求切线长的最小值
(Ⅲ)求|PA|2+|PB|2的最值及此时点P的坐标.
【答案】解:(Ⅰ)由x﹣y+c≥0,得c≥y﹣x,由圆的参数方程得c≥4+2sinθ﹣3﹣2cosθ,所以 ![]()
(Ⅱ)圆心C到直线x+y+1=0的距离为4 ![]() ,切线长的最小值为
,切线长的最小值为 ![]()
(Ⅲ)设P(a,b),则|PA|2+|PB|2=2a2+2b2+2,a2+b2为圆C:(x﹣3)2+(y﹣4)2=4上的点到原点的距离平方,所以最小值为20, ![]() ;最大值为100,
;最大值为100, ![]()
【解析】(Ⅰ)由x﹣y+c≥0,得c≥y﹣x,由圆的参数方程得c≥4+2sinθ﹣3﹣2cosθ,即可求c的范围;(Ⅱ)求出圆心C到直线x+y+1=0的距离为4 ![]() ,利用勾股定理求切线长的最小值;(Ⅲ)设出的是PP(a,b),使要求的式子转化为求圆上的点到原点的距离问题,利用数形结合法求最值.
,利用勾股定理求切线长的最小值;(Ⅲ)设出的是PP(a,b),使要求的式子转化为求圆上的点到原点的距离问题,利用数形结合法求最值.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合 ![]()
(1)求A∩B;
(2)若A∪C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有楼房一幢,室内面积共计180m2 , 拟分割成两类房间作为旅游客房,大房间每间面积为18m2 , 可住游客5名,每名游客每天住宿费40元;小房间每间面积为15m2 , 可以住游客3名,每名游客每天住宿费50元;装修大房间每间需要1000元,装修小房间每间需要600元.如果他只能筹款8000元用于装修,且假定游客能住满客房,他应隔出大房间和小房间各多少间,才能获得最大收益? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={f(x)|f2(x)﹣f2(y)=f(x+y)f(x﹣y),x,y∈R},有下列命题
①若f(x)= ![]() ,则f(x)∈M;
,则f(x)∈M;
②若f(x)=2x,则f(x)∈M;
③f(x)∈M,则y=f(x)的图象关于原点对称;
④f(x)∈M,则对于任意实数x1 , x2(x1≠x2),总有 ![]() <0成立;
<0成立;
其中所有正确命题的序号是 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1﹣DC﹣C1的大小为60°,则AD的长为( ) 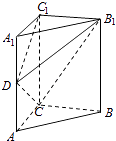
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 的通项公式分别为
的通项公式分别为![]() ,将集合
,将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() ;将集合
;将集合![]()
![]() 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com