
【题目】如图,椭圆W:![]() 的焦距与椭圆Ω:
的焦距与椭圆Ω:![]() +y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
+y2=1的短轴长相等,且W与Ω的长轴长相等,这两个椭圆的在第一象限的交点为A,直线l经过Ω在y轴正半轴上的顶点B且与直线OA(O为坐标原点)垂直,l与Ω的另一个交点为C,l与W交于M,N两点.
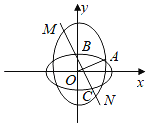
(1)求W的标准方程:
(2)求![]() .
.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】一些选手参加数学竞赛,其中有些选手互相认识,有些选手互相不认识,而任何两个不相识的选手都恰有两个共同的熟人.若![]() 与
与![]() 认识,但没有共同的熟人,求证:
认识,但没有共同的熟人,求证:![]() 、
、![]() 认识的熟人一样多.
认识的熟人一样多.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小店每天以每份5元的价格从食品厂购进若干份食品,然后以每份10元的价格出售.如果当天卖不完,剩下的食品还可以每份1元的价格退回食品厂处理.
(Ⅰ)若小店一天购进16份,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(Ⅱ)小店记录了100天这种食品的日需求量(单位:份),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)小店一天购进16份这种食品,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(ii)以小店当天利润的期望值为决策依据,你认为一天应购进食品16份还是17份?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试确定平面上是否存在满足下述条件的两个不相交的无限点集![]() 、
、![]() :
:
(1)在![]() 中,任何三点不共线,且任何两点的距离至少为1;
中,任何三点不共线,且任何两点的距离至少为1;
(2)任何一个顶点在![]() 中的三角形,其内部均存在一个
中的三角形,其内部均存在一个![]() 中的点,任何一个顶点在
中的点,任何一个顶点在![]() 中的三角形,其内部均存在一个
中的三角形,其内部均存在一个![]() 中的点.
中的点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义在
是定义在![]() 上的偶函数,且对任意的
上的偶函数,且对任意的![]() 恒有
恒有![]() ,已知当
,已知当![]() 时,
时,![]() ,则
,则
①![]() 是函数
是函数![]() 的一个周期;
的一个周期;
②函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
③函数![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ;
;
④![]() 是函数
是函数![]() 的一个对称轴;
的一个对称轴;
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 为
为![]() 内一点,直线
内一点,直线![]() 、
、![]() 、
、![]() 与边
与边![]() 、
、![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() 、
、![]() .设分别以
.设分别以![]() 、
、![]() 为直径的两圆交于点
为直径的两圆交于点![]() 、
、![]() ,分别以
,分别以![]() 、
、![]() 为直径的两圆交于点
为直径的两圆交于点![]() 、
、![]() ,分别以
,分别以![]() 、
、![]() 为直径的两圆交于点
为直径的两圆交于点![]() 、
、![]() .证明:
.证明:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六点共圆.
六点共圆.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com