
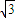 asinωx-acosωx
asinωx-acosωx ,2),(
,2),(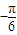 ,-2).
,-2).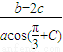 的值.
的值. ),从而求出它的周期.
),从而求出它的周期. =600 ,再根据正弦定理把要求的式子化为
=600 ,再根据正弦定理把要求的式子化为 ,再利用两角和差的正弦、余弦公式进一步化为
,再利用两角和差的正弦、余弦公式进一步化为 ,
, asinωx-acosωx=2asin(ωx-
asinωx-acosωx=2asin(ωx- ),由已知知周期T=2[
),由已知知周期T=2[ -(
-( )]=π=
)]=π= ,∴ω=2.
,∴ω=2. )=1,∵0<A<π,∴-
)=1,∵0<A<π,∴- <2A-
<2A- <
< ,则2A-
,则2A- =
= ,解得A=
,解得A= =60.
=60. =
= =
=
 =
= =2.(也可用B化简)…(12分)
=2.(也可用B化简)…(12分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com