
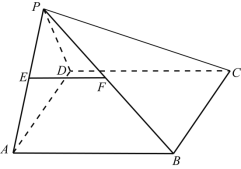
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧面PAD⊥底面ABCD,E为PA的中点,过C,D,E三点的平面与PB交于点F,且PA=PD=AB=2.
(1)证明:![]() ;
;
(2)若四棱锥![]() 的体积为
的体积为![]() ,则在线段
,则在线段![]() 上是否存在点G,使得二面角
上是否存在点G,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)由AB//CD推出CD//平面PAB,利用线面平行的性质可推出CD//EF,又CD⊥AD则![]() ;(2)由面面垂直的性质证明PO⊥平面ABCD,即可根据四棱锥
;(2)由面面垂直的性质证明PO⊥平面ABCD,即可根据四棱锥![]() 的体积及勾股定理求出PO,AD,建立空间直角坐标系,设
的体积及勾股定理求出PO,AD,建立空间直角坐标系,设![]() ,由空间向量法利用
,由空间向量法利用![]() 的余弦值列出方程即可求得
的余弦值列出方程即可求得![]() .
.
(1)证明:由题意得,AB//CD,
又AB平面PAB,CD平面PAB,∴CD//平面PAB.
又CD平面CDEF,平面CDEF∩平面PAB=EF,
∴CD//EF,又CD⊥AD,∴EF⊥AD.
(2)取AD的中点为O,连接PO,![]() PA=PD,
PA=PD,![]() PO⊥AD,
PO⊥AD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO平面PAD,
∴PO⊥平面ABCD,
∴VP-ABCD=![]() AB·AD·PO=
AB·AD·PO=![]() ,则AD·PO=4,
,则AD·PO=4,
又PO2+![]() =4,∴PO=
=4,∴PO=![]() ,AD=2
,AD=2![]() .
.
取BC的中点为H,以OA,OH,OP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则P(0,0,![]() ),B(
),B(![]() ,2,0),D(-
,2,0),D(-![]() ,0,0),C(-
,0,0),C(-![]() ,2,0),
,2,0),
∴![]() =(
=(![]() ,2,-
,2,-![]() ),
),![]() =(0,-2,0).
=(0,-2,0).

假设存在点G,设![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() =(
=(![]() (1+λ),2λ,
(1+λ),2λ,![]() (1-λ)),
(1-λ)),
设平面GCD的法向量为![]() ,
,
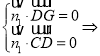
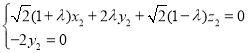 ,可取
,可取![]() ,
,
又平面![]() 的一个法向量
的一个法向量![]() ,二面角G-CD-B为锐角,
,二面角G-CD-B为锐角,
∴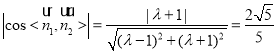 ,解得λ=
,解得λ=![]() 或λ=3(舍).
或λ=3(舍).
![]() 存在点G,使得二面角G-CD-B的余弦值为
存在点G,使得二面角G-CD-B的余弦值为![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
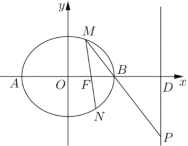
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .(其中
.(其中![]() 为
为![]() 的极小值点)
的极小值点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党的号召,坚决打赢脱贫攻坚战,某地区实行了帮扶单位定点帮扶扶贫村脱贫.为了解该地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
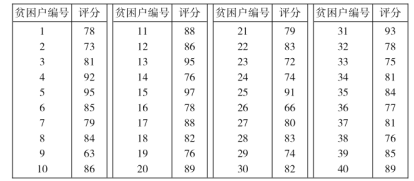
现按贫困户编号从小到大的顺序分组,用系统抽样法从40名贫困户中抽取容量为10的样本.
(1)若在第一分段里随机抽到的第一个样本的评分数据为81,记第二和第十个样本的评分数据分别为a,b,请写出a,b的值;
(2)若10个样本的评分数据分别为92,84,86,78,89,74,83,78,77,89.请你计算所抽到的10个样本的平均数![]() 和方差
和方差![]() ;
;
(3)在(1)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
之间,则满意度等级为“A级”.试应用样本估计总体的思想,用(2)中的样本数据,估计在满意度为“A级”的贫困户中随机地抽取2户,所抽到2户的满意度评分均“超过80”的概率.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
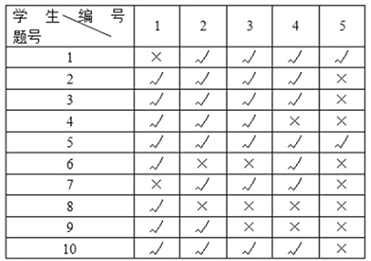
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,平面PBC⊥平面ABC,∠ACB=90°,BC=PC=2,若AC=PB,则三棱锥P﹣ABC体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如下表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
60 44 66 44 21
66 06 58 05 62
61 65 54 35 02
42 35 48 96 32
14 52 41 52 48
92 66 22 15 86
96 63 75 41 99
58 42 36 72 24
A.23B.21C.35D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: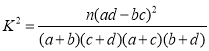 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com