
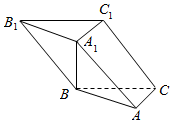
 如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.
如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.分析 (1)推导出AC⊥AB,A1B⊥AC,从而AC⊥平面ABB1A1,由此能证明平面ABB1A1⊥平面ACC1A1.
(2)以B为原点,BA为x轴,在平面ABC中过B作BA的垂线为y轴,BA1为z轴,建立空间直角坐标系,利用向量法能求出二面角A-BB1-C的正切值.
解答 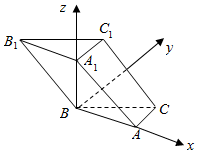 证明:(1)在△ABC中,∵AB2+AC2=BC2,∴AC⊥AB,…(2分)
证明:(1)在△ABC中,∵AB2+AC2=BC2,∴AC⊥AB,…(2分)
又∵A1B⊥AC且A1B、AC是面ABB1A1内的两条相交直线,
∴AC⊥平面ABB1A1,..…(4分)
又AC?平面ACC1A1,
∴平面ABB1A1⊥平面ACC1A1.…(5分)
解:(2)在△ABC中,∵${A_1}{B^2}+A{B^2}=A{A_1}^2$,∴A1B⊥AB,
又∵A1B⊥AC且AB、AC是面ABC内的两条相交直线,∴A1B⊥面ABC,…(7分)
∴以B为原点,BA为x轴,在平面ABC中过B作BA的垂线为y轴,BA1为z轴,
建立如图所示的空间直角坐标系,
则B(0,0,0),A(12,0,0),C(12,5,0),A1(0,0,5),
由$\overrightarrow{B{B_1}}=\overrightarrow{A{A_1}}$,得B1(-12,0,5),…(8分)
取平面ABB1A1的一个法向量$\overrightarrow{{n}_{1}}$=(0,1,0),
设平面BCC1B1的一个法向量$\overrightarrow{n_2}=(x,y,z)$,
由$\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{B{B_1}}=0}\\{\overrightarrow{n_2}•\overrightarrow{BC}=0}\end{array}}\right.$,得 $\left\{\begin{array}{l}-12x+5z=0\\ 12x+5y=0.\end{array}\right.$
取x=5,则$\overrightarrow{n_2}=(5,-12,12)$…(10分)
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|{\overrightarrow{{n}_{1}}}_{\;}|•|\overrightarrow{{n}_{2}}|}$=-$\frac{12}{\sqrt{313}}$,
设A-BB1-C的大小为θ,
则$cosθ=\frac{12}{{\sqrt{313}}}$,$tanθ=\frac{13}{12}$.
∴二面角A-BB1-C的正切值的大小为$\frac{13}{12}$…(12分)
点评 本题考查面面垂直的证明,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | $\frac{47}{5}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤e | B. | 0<a≤e | C. | a≥e | D. | 0<a<$\frac{1}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2$\sqrt{3}$,∠DAB=∠BCD=90°,且AA1=CC1=$\frac{3}{2}$;
如图所示的多面体是由一个以四边形ABCD为地面的直四棱柱被平面A1B1C1D1所截面成,若AD=DC=2,AB=BC=2$\sqrt{3}$,∠DAB=∠BCD=90°,且AA1=CC1=$\frac{3}{2}$;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某种产品表面进行腐蚀性试验,得到腐蚀深度y与腐蚀时间x之间对应的一组数据:
在某种产品表面进行腐蚀性试验,得到腐蚀深度y与腐蚀时间x之间对应的一组数据:| 时间x(s) | 2 | 3 | 4 | 5 | 6 |
| 深度y(μm) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com