
分析 (1)据二次函数的形式设出f(x)的解析式,将已知条件代入,列出方程,令方程两边的对应系数相等解得.
(2)函数g(x)的图象是开口朝上,且以x=m为对称轴的抛物线,分当m≤0时,当0<m<2时,当m≥2时三种情况分别求出函数的最小值,可得答案.
解答 解:(1)设f(x)=a(x+3)(x-5),
∵f(2)=15,∴a(2+3)(2-5)=15,解得:a=-1,
∴函数f(x)的表达式为f(x)=-x2+2x+15;
(2)∵g(x)=(2-2m)x-f(x)=x2-2mx-15,
函数图象是开口朝上,且以x=m为对称轴的抛物线,
当m≤0时,g(x)在[0,2]上为增函数,当x=0时,函数g(x)取最小值-15;
当0<m<2时,g(x)在[0,m]上为减函数,在[m,2]上为增函数,当x=m时,函数g(x)取最小值-m2-15;
当m≥2时,g(x)在[0,2]上为减函数,当x=2时,函数g(x)取最小值-4m-11;
∴函数g(x)在x∈[0,2]的最小值为 $\left\{\begin{array}{l}{-15,m≤0}\\{{-m}^{2}-15,0<m<2}\\{-4m-11,m≥2}\end{array}\right.$.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
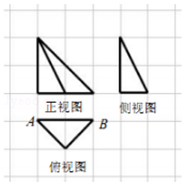 如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的体积记为V1,俯视图绕底边AB所在直线旋转一周形成的几何体的体积记为V2,则V1:V2( )
如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的体积记为V1,俯视图绕底边AB所在直线旋转一周形成的几何体的体积记为V2,则V1:V2( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | mn=1 | B. | mn=-1 | C. | m+n=-1 | D. | m+n=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒大于0 | B. | 恒小于0 | C. | 等于0 | D. | 无法判断 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com