
【题目】从1到9的九个数字中取三个偶数四个奇数,试问:
①能组成多少个没有重复数字的七位数?
②上述七位数中三个偶数排在一起的有几个?
③在①中的七位数中,偶数排在一起、奇数也排在一起的有几个?
④在①中任意两偶数都不相邻的七位数有几个?
【答案】①100800;②14400;③5760;④28800
【解析】
①分步完成:第一步计算在4个偶数中取3个的情况数目,第二步计算在5个奇数中取4个的情况数目,第三步将取出的7个数进行全排列,计算可得答案;
②由①的第一、二步,将3个偶数排在一起,有![]() 种情况,与4个奇数共5个元素全排列,计算可得答案;
种情况,与4个奇数共5个元素全排列,计算可得答案;
③由①的第一、二步,将3个偶数排在一起,有![]() 种情况,4个奇数也排在一起有
种情况,4个奇数也排在一起有![]() 种情况,将奇数与偶数进行全排列计算可得答案;
种情况,将奇数与偶数进行全排列计算可得答案;
④由①的第一、二步,可先把4个奇数取出并排好有![]() 种情况,再将3个偶数分别插入5个空档,有
种情况,再将3个偶数分别插入5个空档,有![]() 种情况,进而由乘法原理,计算可得答案.
种情况,进而由乘法原理,计算可得答案.
解:①分步完成:第一步在4个偶数中取3个,可有![]() 种情况;
种情况;
第二步在5个奇数中取4个,可有![]() 种情况;
种情况;
第三步3个偶数,4个奇数进行排列,可有![]() 种情况,
种情况,
所以符合题意的七位数有![]() 个.
个.
②上述七位数中,三个偶数排在一起的有![]() 个.
个.
③上述七位数中,3个偶数排在一起,4个奇数也排在一起的有![]() 个.
个.
④上述七位数中,偶数都不相邻,可先把4个奇数排好,再将3个偶数分别插入5个空档,共有![]()
![]() 个.
个.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为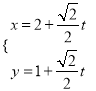 ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学基本公式大赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
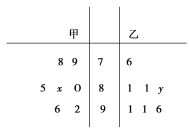
(1)求x和y的值;
(2)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]()
![]() 的成员自驾时,自驾群体的人均通勤时间为
的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 取何值时,公交群体的人均通勤时间等于自驾群体的人均通勤时间?
取何值时,公交群体的人均通勤时间等于自驾群体的人均通勤时间?
(2)已知上班族![]() 的人均通勤时间计算公式为
的人均通勤时间计算公式为![]() ,讨论
,讨论![]() 单调性,并说明其实际意义.
单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为6的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为![]() ,容积为
,容积为![]() .
.
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当![]() 为多少时,容器的容积最大?并求出最大容积.
为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设整数![]() ,对置于
,对置于![]() 个点
个点![]() 及点
及点![]() 处的卡片作如下操作:操作
处的卡片作如下操作:操作![]() :若某个点
:若某个点![]() 处的卡片数不少于3,则可从中取出三张,在三点
处的卡片数不少于3,则可从中取出三张,在三点![]() 、
、![]() 、
、![]() 处各放一张
处各放一张![]() ;操作
;操作![]() :若点
:若点![]() 处的卡片数不少于
处的卡片数不少于![]() ,则可从中取出
,则可从中取出![]() 张,在
张,在![]() 个点
个点![]() 处各放一张。证明:只要放置于这
处各放一张。证明:只要放置于这![]() 个点处的卡片总数不少于
个点处的卡片总数不少于![]() ,则总能通过若干次操作,使得每个点处的卡片数均不少于
,则总能通过若干次操作,使得每个点处的卡片数均不少于![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com