练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，AsinC

    （Ⅰ）求∠B的大小；

    （Ⅱ）求cosA+cosC的最大值．

    【答案】（Ⅰ） ；（Ⅱ）1

    【解析】

    （Ⅰ）由正弦定理得a2+c2=b2+ac，即可求得cosB，则B可求；（Ⅱ）由C=-A，代入cosA+cosC整理为sin（A+），由A的范围求其最大值即可

    （Ⅰ）∵在△ABC中，由正弦定理可得a2+c2=b2+ac．∴a2+c2-b2=ac，

    ∴cosB=，又B

    ∴B=；

    （Ⅱ）由（I）得：C=-A，

    ∴cosA+cosC =cosA+cos（-A）=cosA-cosA+sinA=cosA+sinA=sin（A+），

    ∵A∈（0，），∴A+∈（，π），

    故当A+=时，sin（A+）取最大值1，即c cosA+cosC的最大值为1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某中学在“三关心”（即关心家庭、关心学校、关心社会）的专题中，对个税起征点问题进行了学习调查.学校决定从高一年级800人，高二年级1000人，高三年级800人中按分层抽样的方法共抽取13人进行谈话，其中认为个税起征点为3000元的有3人，认为个税起征点为4000元的有6人，认为个税起征点为 5000元的有4人.

    （1）求高一年级、高二年级、高三年级分别抽取多少人？

    （2）从13人中选出3人，求至少有1人认为个税起征点为4000元的概率；

    （3）记从13人中选出3人中认为个税起征点为4000元的人数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}，{bn}中，a1=2，b1=4且an ， bn ， an+1成等差数列，bn ， an+1 ， bn+1成等比数列（n∈N*）
    （1）求a2 ， a3 ， a4及b2 ， b3 ， b4；由此归纳出{an}，{bn}的通项公式，并证明你的结论．
    （2）若cn=log2（），Sn=c1+c2+…+cn ， 试问是否存在正整数m，使Sm≥5，若存在，求最小的正整数m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AB是半圆O的直径，C是半圆O上除A、B外的一个动点，DC垂直于半圆O所在的平面，DC∥EB，DC=EB，AB=4，tan∠EAB= ．
    证明：平面ADE⊥平面ACD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=-a2 lnx+x2-ax（a∈R）．

    （1）试讨论函数f（x）的单调性：

    （2）若函数f（x）在区间（1，e）中有两个零点，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在下列向量组中，可以把向量＝(3，2)表示出来的是(　 　)

    A. ＝(0，0)，＝(1，2)B. ＝(－1，2)，＝(5，－2)

    C. ＝(3，5)，＝(6，10)D. ＝(2，－3)，＝(－2，3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， a1=1，且nan+1=2Sn（n∈N*），数列{bn}满足b1= ， b2= ， 对任意n∈N* ， 都有bn+12=bnbn+2 ．
    求数列{an}、{bn}的通项公式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥P﹣ABCD的底面为平行四边形，PD⊥平面ABCD，M为PC中点．

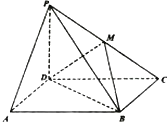
    （1）求证：AP∥平面MBD；

    （2）若AD⊥PB，求证：BD⊥平面PAD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C对应的边分别是a，b，c，已知cos2A﹣3cos（B+C）=1．

    （1）求角A的大小；

    （2）若△ABC的面积S=5，b=5，求sinBsinC的值．

    查看答案和解析>>

    同步练习册答案