
【题目】在![]() 中,角
中,角![]() 所对的边分别是
所对的边分别是![]() ,已知
,已知![]() 且
且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:利用正弦定理进行角转边,然后再利用余弦定理求出角C,已知两角及一角所对的边利用正弦定理解三角形,求出边a,由sinA求出cosA,利用三角形的内角和关系利用角A、C表示sinB,借助两角和公式求出sinB ,最后利用面积公式求出三角形的面积.
试题解析:
(Ⅰ)由![]() ,且
,且![]()
又根据正弦定理,得![]() ,
,
化简得, ![]() ,故
,故![]() ,
,
所以![]() .
.
(Ⅱ)由![]() ,
, ![]() ,
, ![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,从而
,从而![]() ,
,
故![]() ,
,
所以![]() 的面积为
的面积为![]() .
.
【点精】利用正弦定理和余弦定理及三角形面积公式解斜三角形是高考高频考点,利用正弦定理和余弦定理进行边转角或角转边是常用的方法,已知两边及其夹角求第三边或已知三边求任意角使用于心定理,已知两角及任意边或已知两边及一边所对的角借三角形用正弦定理.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
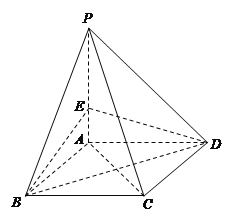
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() 是棱
是棱![]() 上的一个动点.
上的一个动点.
(Ⅰ)若![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的前n项和为Sn , 已知对任意的n∈N+ , 点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数的图象上.
(1)求r的值.
(2)当b=2时,记bn=2(log2an+1)(n∈N+),证明:对任意的n∈N+,不等式成立 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )??
)??
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女子善织,日益功,疾,初日织五尺,今一月织九匹三丈(1匹=40尺,一丈=10尺),问日益几何?”其意思为:“有一女子擅长织布,每天比前一天更加用功,织布的速度也越来越快,从第二天起,每天比前一天多织相同量的布,第一天织5尺,一月织了九匹三丈,问每天增加多少尺布?”若一个月按30天算,则每天增加量为( ) 
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据影院的经营经验,当每张票价不超过10元时,票可全售出;当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院定一个合适的票价,需符合的基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放一场电影的成本费用支出为5750元,票房的收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入),问:
(1)把y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,票价定为多少时,放映一场的净收人最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某刻考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:
(单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:

(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为120分,物理平均分为92,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,
, ![]()
参考数据: ![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com