
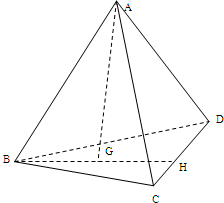
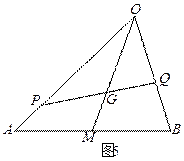 如图5,
如图5,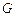 是△
是△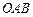 的重心,
的重心,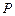 、
、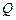 分别是边
分别是边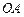 、
、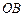 上的动点,且
上的动点,且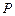 、
、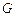 、
、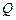 三点共线.(1)设
三点共线.(1)设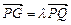 ,将
,将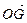 用
用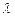 、
、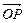 、
、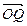 表示;
表示;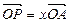 ,
,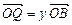 ,证明:
,证明: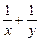 是定值;
是定值;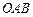 与△
与△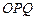 的面积分别为
的面积分别为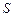 、
、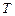 .求
.求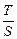 的取值范围.
的取值范围.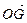
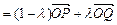 (Ⅱ)
(Ⅱ) 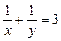 (Ⅲ)
(Ⅲ)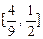
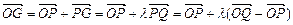
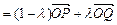 .…2分
.…2分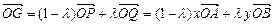 ;①
;①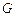 是△
是△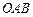 的重心,
的重心,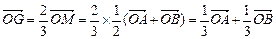 ②…4分
②…4分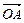 、
、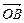 不共线,∴由①、②,得
不共线,∴由①、②,得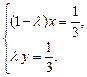 …6分
…6分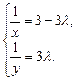 ,∴
,∴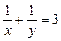 (定值).…………………8分
(定值).…………………8分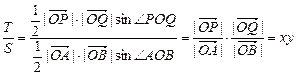 .……………………10分
.……………………10分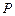 、
、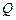 的定义知
的定义知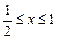 ,
,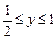 ,
,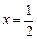 时,
时,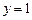 ;
;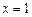 时,
时,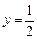 .此时,均有
.此时,均有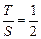 .
.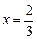 时,
时,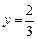 .此时,均有
.此时,均有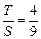 .
.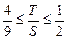 .
.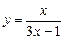 ,
,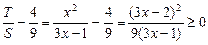 ,∴
,∴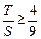 .…………………………12分
.…………………………12分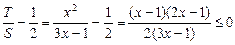 ,∴
,∴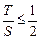 .
.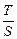 的取值范围
的取值范围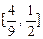 .………………………………14分
.………………………………14分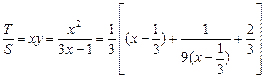 ,
,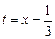 ,则
,则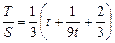 ,其中
,其中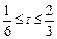 .
.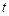 的函数
的函数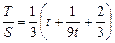 在闭区间
在闭区间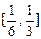 上单调递减,在闭区间
上单调递减,在闭区间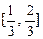 上单调递增.………………………………12分
上单调递增.………………………………12分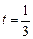 时,
时,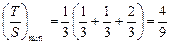 .
.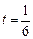 或
或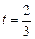 时,均有
时,均有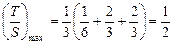 .
.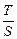 的取值范围
的取值范围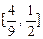 .…………………………14分
.…………………………14分

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| AB |
| AC |
| AD |
| AG |
| AB |
| AC |
| AD |
| AG |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com