
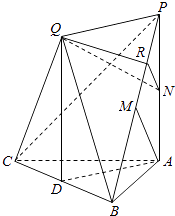
【题目】如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(1)求证:PA∥平面QBC;
(2)PQ⊥平面QBC,求二面角Q﹣PB﹣A的余弦值.
【答案】
(1)解:证明:过点Q作QD⊥BC于点D,
∵平面QBC⊥平面ABC,∴QD⊥平面ABC,
又∵PA⊥平面ABC,
∴QD∥PA,又∵QD平面QBC,PA平面QBC,
∴PA∥平面QBC.
(2)解:方法一:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连接AD,则AD⊥BC,
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.
设PA=2a,
∴ ![]() ,PB=2
,PB=2 ![]() a,∴
a,∴ ![]() .
.
过Q作QR⊥PB于点R,
∴QR= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
取PB中点M,连接AM,取PA的中点N,连接RN,
∵PR= ![]() ,
, ![]() ,∴MA∥RN.
,∴MA∥RN.
∵PA=AB,∴AM⊥PB,∴RN⊥PB.
∴∠QRN为二面角Q﹣PB﹣A的平面角.
连接QN,则QN= ![]() =
= ![]() =
= ![]() .又
.又 ![]() ,
,
∴cos∠QRN= ![]() =
= 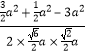 =
= ![]() .
.
即二面角Q﹣PB﹣A的余弦值为 ![]() .
.
方法二:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连AD,则AD⊥BC.
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.
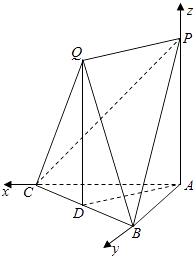
分别以AC、AB、AP为x、y、z轴建立空间直角坐标系O﹣xyz.
不妨设PA=2,则Q(1,1,2),B(0,2,0),P(0,0,2),
设平面QPB的法向量为 ![]() .
.
∵ ![]() =(1,1,0),
=(1,1,0), ![]() =(0,2,﹣2).
=(0,2,﹣2).
∴ ![]() 令x=1,则y=z=﹣1.
令x=1,则y=z=﹣1.
又∵平面PAB的法向量为 ![]() .
.
设二面角Q﹣PB﹣A为θ,则|cosθ|= ![]() =
= ![]() =
= ![]()
又∵二面角Q﹣PB﹣A是钝角
∴ ![]() .
.
【解析】(1)利用线面垂直的性质定理及线面平行的判定定理即可证明;(2)方法一:利用三角形的中位线定理及二面角的平面角的定义即可求出.方法二:通过建立空间直角坐标系,利用平面的法向量所成的夹角来求两平面的二面角的平面角.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
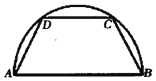
【题目】如图,将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状,下底AB是半圆的直径,上底CD的端点在圆周上,则所得梯形面积的最大值为( )
A. 3![]() B. 3
B. 3![]() C. 5
C. 5![]() D. 5
D. 5![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(x2+tx+2)(t为常数,且﹣2 ![]() <t<2
<t<2 ![]() ).
).
(1)当x∈[0,2]时,求函数f(x)的最小值(用t表示);
(2)是否存在不同的实数a,b,使得f(a)=lga,f(b)=lgb,并且a,b∈(0,2).若存在,求出实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差数列,若存在,求出所有满足条件的
)成等差数列,若存在,求出所有满足条件的![]() ,
,![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知任意角θ以x轴非负半轴为始边,若终边经过点P(x0 , y0),且|OP|=r(r>0),定义sicosθ= ![]() ,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
,称“sicosθ”为“正余弦函数”.对于正余弦函数y=sicosx,有同学得到如下结论: ①该函数是偶函数;
②该函数的一个对称中心是( ![]() ,0);
,0);
③该函数的单调递减区间是[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z.
],k∈Z.
④该函数的图象与直线y= ![]() 没有公共点;
没有公共点;
以上结论中,所有正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣1.
(1)对于任意的1≤x≤2,不等式4m2|f(x)|+4f(m)≤|f(x﹣1)|恒成立,求实数m的取值范围;
(2)若对任意实数x1∈[1,2].存在实数x2∈[1,2],使得f(x1)=|2f(x2)﹣ax2|成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=aln(x2+1)+bx,g(x)=bx2+2ax+b,(a>0,b>0).已知方程g(x)=0有两个不同的非零实根x1 , x2 .
(1)求证:x1+x2<﹣2;
(2)若实数λ满足等式f(x1)+f(x2)+3a﹣λb=0,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,sinx),
=(1,sinx), ![]() =(cos(2x+
=(cos(2x+ ![]() ),sinx),函数f(x)=
),sinx),函数f(x)= ![]()
![]() ﹣
﹣ ![]() cos2x
cos2x
(1)求函数f(x)的解析式及其单调递增区间;
(2)当x∈[0, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程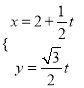 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() .
.
(1)把直线![]() 的参数方程化为极坐标方程,把曲线
的参数方程化为极坐标方程,把曲线![]() 的极坐标方程化为普通方程;
的极坐标方程化为普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交点的极坐标(
交点的极坐标(![]() ≥0,0≤
≥0,0≤![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com