解:(1)因为
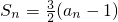
,n∈N
+,所以
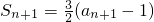
.
两式相减,得
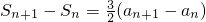
,即
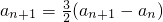
,
∴a
n+1=3a
n,n∈N
+.(3分)
又
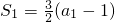
,即
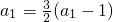
,所以a
1=3.
∴a
n是首项为3,公比为3的等比数列.
从而a
n的通项公式是a
n=3
n,n∈N
+.(6分)
(2)设y=a
i=3
i∈A
n,i≤n,n∈N
+.
当i=2k,k∈N
+时,
∵y=3
2k=9
k=(8+1)
k=C
k08
k+C
k18
k-1++C
kk-18+C
kk=4×2(C
k08
k-1+C
k18
k-2++C
kk-1)+1,∴y∈B.(9分)
当i=2k-1,k∈N
+时,
∵y=3
2k-1=3×(8+1)
k-1=3×(C
k-108
k-1+C
k-118
k-2++C
k-1k-28+C
k-1k-1)
=4×6(C
k-108
k-2+C
k-118
k-3++C
k-1k-2)+3,∴y∉B.(12分)
又∵集合A
n含n个元素,
∴在集合A
n中随机取一个元素y,有y∈B的概率p(n)=

.(14分)
分析:(1)直接根据a
n和S
n的关系:a
n=S
n-S
n-1 (n≥2)求解数列的通项公式(注意检验n=1是否成立)
(2)对i取奇数和偶数两种情况分别讨论求出对应的集合A
n,再求出对应的p(n)的表达式即可.
点评:本题考查了已知前n项和为S
n求数列{a
n}的通项公式,根据a
n和S
n的关系:a
n=S
n-S
n-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:a
n=S
n-S
n-1 (n≥1);若不成立,则通项公式为分段函数.

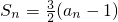 ,n∈N+.
,n∈N+.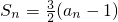 ,n∈N+,所以
,n∈N+,所以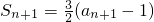 .
.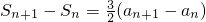 ,即
,即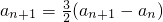 ,
,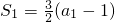 ,即
,即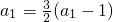 ,所以a1=3.
,所以a1=3. .(14分)
.(14分)
