
分析 讨论f(x)在(-∞,1]递增,区间(-a,2a)⊆(-∞,1],求得f(x)的导数,令f′(x)≥0在区间(-a,2a)上恒成立,即有f′(-a)≥0且f′(2a)≥0;若f(x)在(-∞,+∞)递增,则f(x)在x>1递增,求得导数,令导数大于等于0,可得a的范围;注意-$\frac{1}{3}$+$\frac{1-a}{2}$+a-$\frac{4}{3}$≤(a-1)ln1+$\frac{1}{2}$-a,解不等式求交集,即可得到所求范围.
解答 解:当x≤1时,f(x)=-$\frac{1}{3}$x3+$\frac{1-a}{2}$x2+ax-$\frac{4}{3}$的导数为f′(x)=-x2+(1-a)x+a,
若f(x)在区间(-a,2a)上单调递增,且2a≤1,
则f′(x)≥0在区间(-a,2a)上恒成立,
即有x2-(1-a)x-a≤0,
可得(-a)2-(1-a)(-a)-a≤0,且(2a)2-2(1-a)a-a≤0,
解得0<a≤$\frac{1}{2}$;①
若f(x)在(-∞,+∞)递增,
即有f(x)在(1,+∞)递增,
即有f(x)=(a-1)lnx+$\frac{1}{2}$x2-ax的导数$\frac{a-1}{x}$+x-a≥0在(1,+∞)恒成立.
即有(x-1)(x-a+1)≥0在(1,+∞)恒成立.
即有a-1≤1,即a≤2;②
又-$\frac{1}{3}$+$\frac{1-a}{2}$+a-$\frac{4}{3}$≤(a-1)ln1+$\frac{1}{2}$-a,
解得a≤$\frac{10}{9}$.③
由①②③可得0<a≤$\frac{10}{9}$.
故答案为:(0,$\frac{10}{9}$].
点评 本题考查分段函数的单调性的判断,考查导数的运用:求单调性,考查分类讨论思想方法,考查化简整理能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | l⊥α | B. | l∥α | C. | l?α或l⊥α | D. | l∥α或l?α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
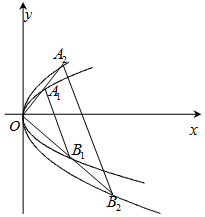 如图,过原点O引两条直线l1,l2与抛物线W1:y2=2px和W2:y2=4px(其中P为常数,p>0)分别交于四个点A1,B1,A2,B2.
如图,过原点O引两条直线l1,l2与抛物线W1:y2=2px和W2:y2=4px(其中P为常数,p>0)分别交于四个点A1,B1,A2,B2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 实验操作 | |||||
| 不合格 | 合格 | 良好 | 优秀 | ||
| 体 能 测 试 | 不合格 | 0 | 0 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 优秀 | 1 | 2 | 3 | 6 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -log36 | D. | -log38 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com